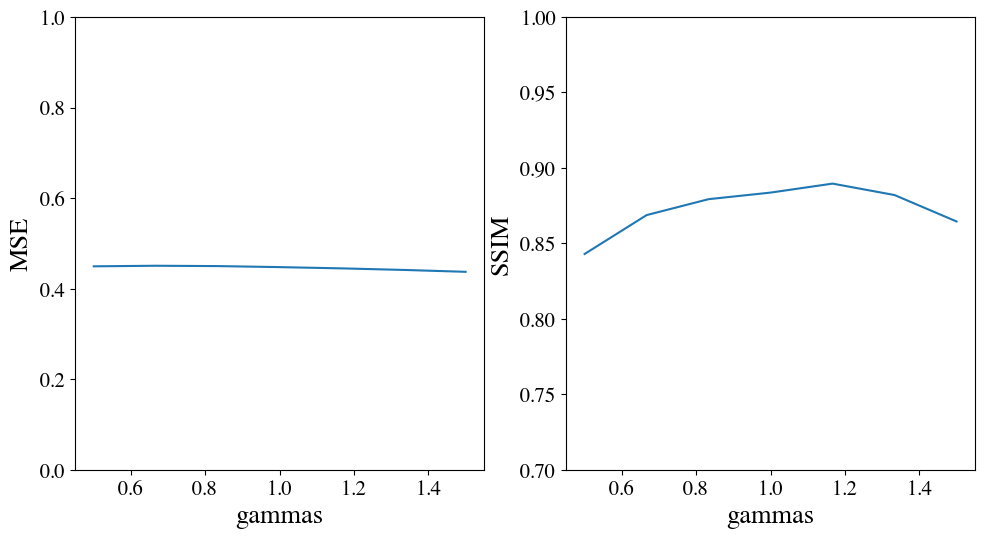
tl;dr : On essaie ici de deviner le transfert des voix entre les choix effectués entre deux scrutins d'un vote (ici les élections présidentielles 2022 en France) par une méthode d'apprentissage automatique.

Afin d'analyser les résultats des élections, par exemple les dernières élections présidentielles de 2022 en France, et de mieux comprendre la dynamique des choix de vote entre les différents groupes de population, il peut être utile d'utiliser des outils d'apprentissage automatique pour inférer des structures à première vue cachées dans la masse des données. En particulier, inspiré par cet article du Monde, on peut se poser la question de savoir si on peut extraire depuis les données brutes des élections une estimation du report de voix entre les choix de vote au premier tour et ceux qui sont effectués au deuxième tour.
Pour cela, parmi les outils mathématiques de l'apprentissage automatique, nous allons utiliser des probabilités. Cette théorie va nous permettre d'exprimer le fait que les résultats tels qu'ils sont obtenus peuvent présenter une variabilité mais que celle-ci réelle résulte de préférences de chaque individu dans la population votante. En particulier, on peut considérer que chaque individu va avoir une préférence, graduée entre $0=0\%$ et $1=100\%$ pour chacun des choix (candidats, nul, blanc, abstention) au premier et second tour. Ainsi, les votes effectués vont correspondre à la réalisation de ces préférences.
Bien sûr, le vote reste secret et on n'a pas accès au vote de chaque individu et encore moins à ses préférences. Mais comme chaque bureau de vote présente des variabilités liées au contexte local et qui fait que cette population locale a une préférence pour certains choix plutôt que d'autres, on peut considérer chaque bureau de vote comme une population individuelle pour lequel nous allons essayer de prédire les résultats du vote au deuxième tour. En exploitant les irrégularités locales, bureau de vote par bureau de vote, nous allons pouvoir prédire (le mieux possible) le report des votes individuel (de chaque individu tel qu'il passe d'un vote à un autre, par exemple de "Hidalgo" à "Macron"). Nous allons en particulier montrer une prédiction très correcte des données du second tour à partir de ceux du premier, montrant la plausibilité d'une telle hypothèse :
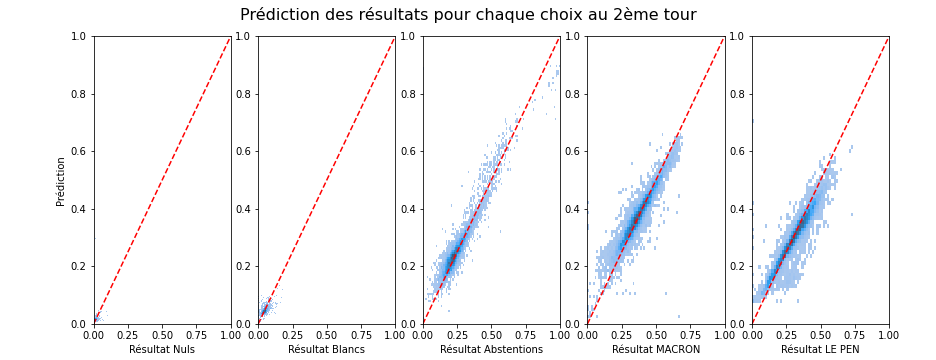
C'est à ma connaissance une contribution originale (jusqu'à ce qu'une bonne âme veuille bien me donner un lien vers une méthode existante similaire qui me permette de correctement la citer...) que nous allons exploiter ici. Cette prédiction, si elle est efficace (et on va montrer qu'elle est en moyenne correctement prédite avec moins de 2 points de pourcentages d'erreur près), peut donner une idée du transfert de vote entre les deux tours qui a lieu en fonction des préférences des votes de chaque individu.
Nous allons dans la suite montrer comment on peut estimer le pourcentage de chances d'exprimer une voix pour un candidat ou pour l'autre en fonction du choix qu'on a exprimé au premier tour:
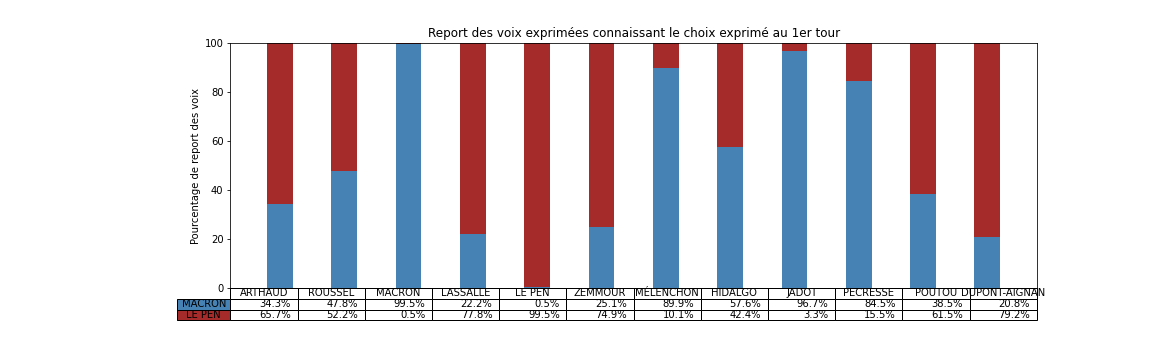
Comme on le verra plus bas, ce tableau montre des tendances claires, par exemple que si on a voté "Macron", "Jadot", "Hidalgo" ou "Pécresse" au premier tour, alors on va certainement voter "Macron" au deuxième tour. Ces électeurs se montrent particulièrement consensuel et suivent le « pacte républicain » mise en place pour faire un "barrage" au Front National (en suivant le terme consacré). Il montre aussi que si on a voté "Le Pen" ou "Dupont-Aignan" au premier tour alors on va voter Le Pen au deuxième, un clair vote de suivi.
Connaissant les couleurs politiques d'autres candidats du premier tour, on peut être surpris que les électeurs de "Arthaud", "Roussel", "Lassalle" ou "Poutou" ont majoritairement choisi "Le Pen" au deuxième tour, signifiant alors un rejet du candidat Macron. Les électeurs de Zemmour sont aussi partagés, signifiant un rejet des deux alternatives. Ce résultat est à prendre avec des pincettes car ces derniers candidats ont obtenu moins de votes et donc que le processus d'inférence est forcément moins précis car il y a moins de données disponibles.
En résumé, cette analyse donne des tendances en fonction des choix exprimés au premier tour:
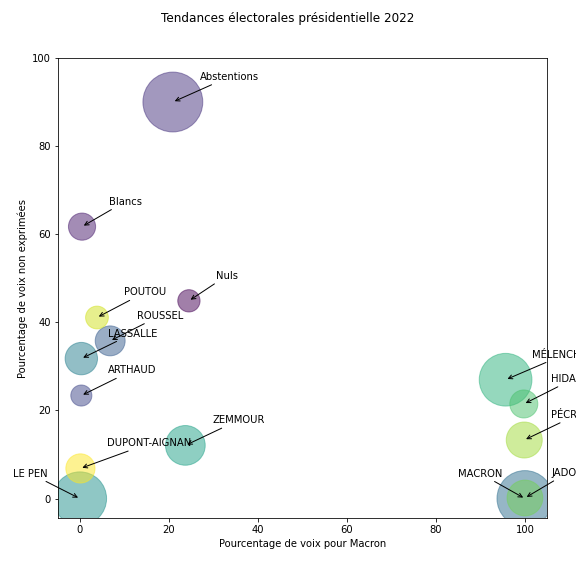 qui montre une nette séparation des groupes de vote.
qui montre une nette séparation des groupes de vote.
Read more…









 qui montre une nette séparation des groupes de vote.
qui montre une nette séparation des groupes de vote.