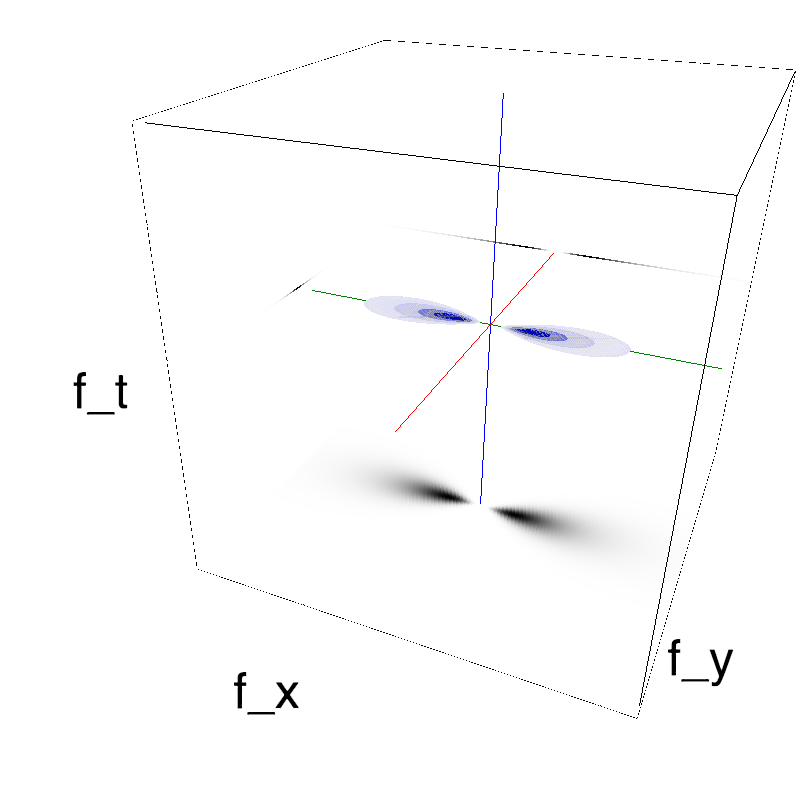
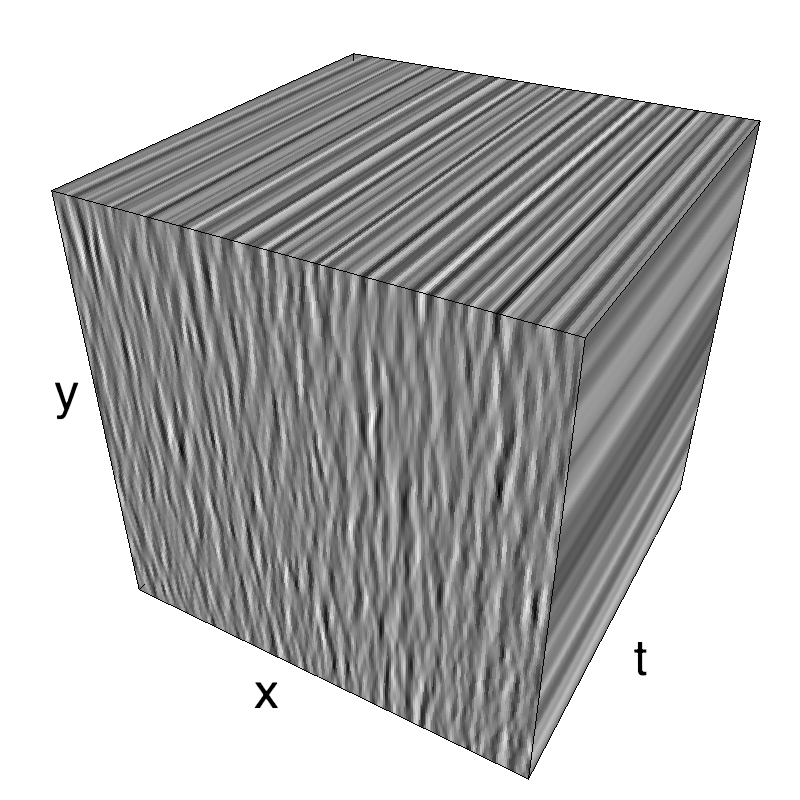
Static Motion Clouds

Source

Motion Clouds were originally defined as moving textures controlled by a few parameters. The library is also capable to generate a static spatial texture. Herein I describe a solution to generate a single static frame.

There are multiple solutions, and the simplest is perhaps to generate a movie that does not move. This means that the mean velocity $(V_X, V_Y)$ is null $=(0, 0)$ but also that there is no noise in the definition of the speed plane. This is defined by $B_V=0$, that is, that all the energy is concentrated on the spped plane:

In [1]:
import MotionClouds as mc
fx, fy, ft = mc.get_grids(mc.N_X, mc.N_Y, mc.N_frame)
name = 'static'
env = mc.envelope_gabor(fx, fy, ft, V_X=0., V_Y=0., B_V=0)
mc.figures(env, name)
mc.in_show_video(name)

/usr/local/lib/python3.7/site-packages/vispy/visuals/isocurve.py:22: UserWarning: VisPy is not yet compatible with matplotlib 2.2+
  warnings.warn("VisPy is not yet compatible with matplotlib 2.2+")
No description has been provided for this image
No description has been provided for this image

As such, all frames are the same and it suffices to take one of them.

Note that as a matter of fact there is a "mathematical issue" here: if we define $B_V = 0$ in our implementation we need to take care of the fact that the formula for the Gaussian doest not give a "dividion by zero" error. The MotionClouds code takes this possibility into accountin the mc.envelope_speed function:

In [2]:
help(mc.envelope_speed)

Help on function envelope_speed in module MotionClouds:

envelope_speed(fx, fy, ft, V_X=1.0, V_Y=0.0, B_V=0.5)
    Returns the speed envelope:
    selects the plane corresponding to the speed ``(V_X, V_Y)`` with some bandwidth ``B_V``.
    
    * (V_X, V_Y) = (0,1) is downward and  (V_X, V_Y) = (1, 0) is rightward in the movie.
    * A speed of V_X=1 corresponds to an average displacement of 1/N_X per frame.
    To achieve one spatial period in one temporal period, you should scale by
    V_scale = N_X/float(N_frame)
    If N_X=N_Y=N_frame and V=1, then it is one spatial period in one temporal
    period. It can be seen along the diagonal in the fx-ft face of the MC cube.
    
    A special case is used when ``B_V=0``, where the ``fx-ft`` plane is used as
    the speed plane: in that case it is desirable to set ``(V_X, V_Y)`` to ``(0, 0)``
    to avoid aliasing problems.
    
    Run the 'test_speed' notebook to explore the speed parameters, see
    https://neuralensemble.github.io/MotionClouds/posts/testing-speed.html

However, this solution is not the most elegant and one could also just state that N_frame is 1 (that is, that the movie consists of only one frame).

The library is made such that this will also work in this slightly degenerate mode:

In [3]:
mc.N_frame=1
fx, fy, ft = mc.get_grids(mc.N_X, mc.N_Y, mc.N_frame)
name = 'static'
env = mc.envelope_gabor(fx, fy, ft, V_X=0., V_Y=0., B_V=0)
z = mc.rectif(mc.random_cloud(env))
print(z.shape)
z = z.reshape((mc.N_X, mc.N_Y))

(256, 256, 1)

Note that in that case, you need to reshape your matrix to one dimension. Using this numpy array, you can now simply plot it:

In [4]:
import matplotlib.pyplot as plt
%matplotlib inline
fig, ax = plt.subplots(figsize=(10,10))
_ = ax.imshow(z.T, cmap=plt.gray())
No description has been provided for this image

a simple application: defining a set of stimuli with different orientation bandwidths

In [5]:
import numpy as np
import MotionClouds as mc
import matplotlib.pyplot as plt
downscale = 1
fx, fy, ft = mc.get_grids(mc.N_X/downscale, mc.N_Y/downscale, 1)


N_theta = 6
bw_values = np.pi*np.logspace(-2, -5, N_theta, base=2)
fig_width = 21


fig, axs = plt.subplots(1, N_theta, figsize=(fig_width, fig_width/N_theta))
for i_ax, B_theta in enumerate(bw_values):
    mc_i = mc.envelope_gabor(fx, fy, ft, V_X=0., V_Y=0., B_V=0, theta=np.pi/2, B_theta=B_theta)
    im = mc.random_cloud(mc_i)
                
    axs[i_ax].imshow(im[:, :, 0], cmap=plt.gray())
    axs[i_ax].text(5, 29, r'$B_\theta=%.1f$°' % (B_theta*180/np.pi), color='white', fontsize=32)
    axs[i_ax].set_xticks([])
    axs[i_ax].set_yticks([])
plt.tight_layout()
fig.subplots_adjust(hspace = .0, wspace = .0, left=0.0, bottom=0., right=1., top=1.)

#import os
#fig.savefig(os.path.join('../figs', 'orientation_tuning.png'))
No description has been provided for this image