Implementing a retinotopic transform using `grid_sample` from pyTorch

Implementing a retinotopic transform using grid_sample from pyTorch

The grid_sample transform is a powerful function which allows to transform any input image into a new topology. It is notably used in Spatial Transformer Networks for instance to learn CNN to be invariant to affine transforms. We used it recently in a publication What You See Is What You Transform: Foveated Spatial Transformers as a Bio-Inspired Attention Mechanism by Ghassan Dabane et al.

The use of grid_sample can b etedious and here, we show how to use it to create a log-polar transform of the image and create the following figure:

Retinotopy

A picture (extract from the painting "The Ambassadors" by Hans Holbein the Younger can be represented on a regular grid represented by vertical (red) and horizontal (blue) lines. Retinotopy transforms this grid, and in particular the area representing the fovea (shaded gray) is over-represented. Applied to the original image of the portrait, the image is strongly distorted and represents more finally the parts under the axis of sight (here the mouth).

Read more…

Elections présidentielles 2022: estimation du transfert de voix

tl;dr : On essaie ici de deviner le transfert des voix entre les choix effectués entre deux scrutins d'un vote (ici les élections présidentielles 2022 en France) par une méthode d'apprentissage automatique.

DOI

Afin d'analyser les résultats des élections, par exemple les dernières élections présidentielles de 2022 en France, et de mieux comprendre la dynamique des choix de vote entre les différents groupes de population, il peut être utile d'utiliser des outils d'apprentissage automatique pour inférer des structures à première vue cachées dans la masse des données. En particulier, inspiré par cet article du Monde, on peut se poser la question de savoir si on peut extraire depuis les données brutes des élections une estimation du report de voix entre les choix de vote au premier tour et ceux qui sont effectués au deuxième tour.

Pour cela, parmi les outils mathématiques de l'apprentissage automatique, nous allons utiliser des probabilités. Cette théorie va nous permettre d'exprimer le fait que les résultats tels qu'ils sont obtenus peuvent présenter une variabilité mais que celle-ci réelle résulte de préférences de chaque individu dans la population votante. En particulier, on peut considérer que chaque individu va avoir une préférence, graduée entre $0=0\%$ et $1=100\%$ pour chacun des choix (candidats, nul, blanc, abstention) au premier et second tour. Ainsi, les votes effectués vont correspondre à la réalisation de ces préférences.

Bien sûr, le vote reste secret et on n'a pas accès au vote de chaque individu et encore moins à ses préférences. Mais comme chaque bureau de vote présente des variabilités liées au contexte local et qui fait que cette population locale a une préférence pour certains choix plutôt que d'autres, on peut considérer chaque bureau de vote comme une population individuelle pour lequel nous allons essayer de prédire les résultats du vote au deuxième tour. En exploitant les irrégularités locales, bureau de vote par bureau de vote, nous allons pouvoir prédire (le mieux possible) le report des votes individuel (de chaque individu tel qu'il passe d'un vote à un autre, par exemple de "Hidalgo" à "Macron"). Nous allons en particulier montrer une prédiction très correcte des données du second tour à partir de ceux du premier, montrant la plausibilité d'une telle hypothèse :

Prédiction du transfert des voix

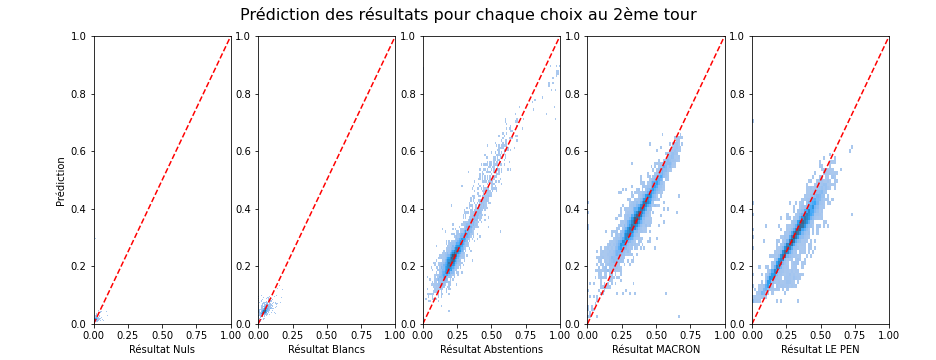
C'est à ma connaissance une contribution originale (jusqu'à ce qu'une bonne âme veuille bien me donner un lien vers une méthode existante similaire qui me permette de correctement la citer...) que nous allons exploiter ici. Cette prédiction, si elle est efficace (et on va montrer qu'elle est en moyenne correctement prédite avec moins de 2 points de pourcentages d'erreur près), peut donner une idée du transfert de vote entre les deux tours qui a lieu en fonction des préférences des votes de chaque individu.

Nous allons dans la suite montrer comment on peut estimer le pourcentage de chances d'exprimer une voix pour un candidat ou pour l'autre en fonction du choix qu'on a exprimé au premier tour:

Transfert des voix

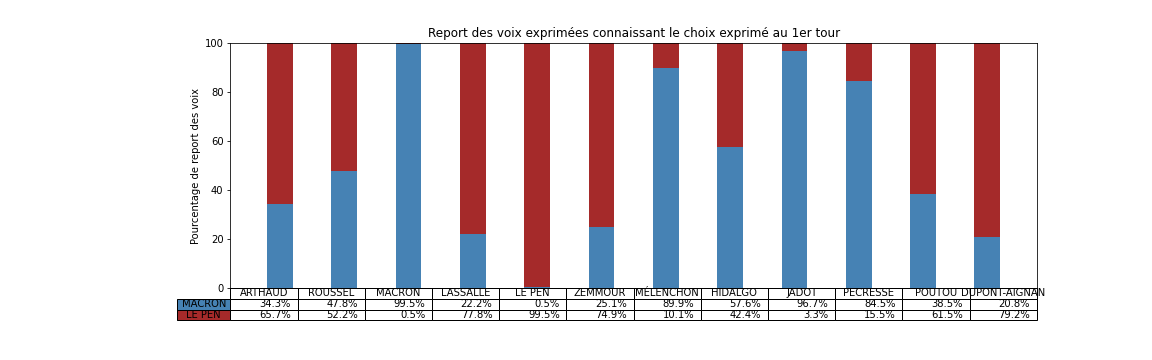
Comme on le verra plus bas, ce tableau montre des tendances claires, par exemple que si on a voté "Macron", "Jadot", "Hidalgo" ou "Pécresse" au premier tour, alors on va certainement voter "Macron" au deuxième tour. Ces électeurs se montrent particulièrement consensuel et suivent le « pacte républicain » mise en place pour faire un "barrage" au Front National (en suivant le terme consacré). Il montre aussi que si on a voté "Le Pen" ou "Dupont-Aignan" au premier tour alors on va voter Le Pen au deuxième, un clair vote de suivi.

Connaissant les couleurs politiques d'autres candidats du premier tour, on peut être surpris que les électeurs de "Arthaud", "Roussel", "Lassalle" ou "Poutou" ont majoritairement choisi "Le Pen" au deuxième tour, signifiant alors un rejet du candidat Macron. Les électeurs de Zemmour sont aussi partagés, signifiant un rejet des deux alternatives. Ce résultat est à prendre avec des pincettes car ces derniers candidats ont obtenu moins de votes et donc que le processus d'inférence est forcément moins précis car il y a moins de données disponibles.

En résumé, cette analyse donne des tendances en fonction des choix exprimés au premier tour: 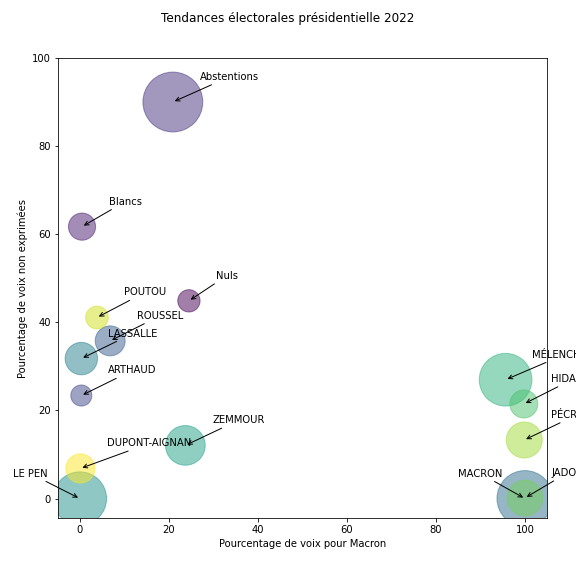Transfert des voix qui montre une nette séparation des groupes de vote.

Read more…

COSYNE reviewer feedback

tl;dr : Crowd-sourcing raw scores for your COSYNE reviewer feedback.

Following that message:

Dear community,

COSYNE is a great conference which plays a pivotal role in our field. If you have submitted an abstract (or several) you have recently received your scores. I am not affiliated to COSYNE - yet willing to contribute in some way: I would like to ask one minute of your time to report the raw scores from your reviewers. I will summarize in a few lines the results in one week time (11/02). The more numerous your feedbacks the better their precision!

Thanks!

As of 2022-02-20, I had received $N = 98$ answers from the google form (out of them, $95$ are valid) out of the $881$ submitted abstracts. In short, the result is that the total score $S$ is simply the linear sum of the scores $s_i$ given by each reviewer $i$ relatively weighted by the confidence levels $\pi_i$ (as stated in the email we received from the chairs):

$$ S = \frac{ \sum_i \pi_i\cdot s_i}{\sum_i \pi_i} $$

Or if you prefer $$ S = \sum_i \frac{\pi_i}{\sum_j \pi_j} \cdot s_i $$

We deduce from that formula that the threshold is close to $6.34$ this year:

2022-02-11_COSYNE-razor

More details in the notebook (or directly in this post) which can also be forked here and interactively modified on binder.

EDIT: On 2022-02-20, I have updated the notebook to account for new answers, I have now received $N = 98$ answers (out of them, $95$ are valid), yet nothing changed qualitatively. On 2022-02-11, I had received $N = 82$ answers from the google form (out of them, $79$ are valid) and the estimated threshold wass close to $6.05$.

Read more…

Dreamachine

It's at the MIAM (Miam Musée International des Arts Modestes) in Sète, France, that I could for the first time experience really the Dreamachine. It's an optical system which consists of a central light which is periodically occluded by a rotating (cardboard?) cylinder.

The magic of it is that the frequency of occlusion is around $12$ Hz, an important resonant state for sensory system. For the first time, I could really try it out at the MIAM - the important point being to close your lids and rest quiet while looking at the stroboscopic light source. Surprisingly, you see the emergence of "psychedelic patterns" (of course, less than in hippie's movies) yet of the order of the color pattern that may arise in Benham's Disk.

It's difficult to reproduce this pattern on a screen, yet it is still possible to give an impression of it. The goal is here :

  • to generate a complex visual stimulation flickering on average at $12$ Hz

  • to project it on a retinotopic space to maximise the "psychelic" effect

retino_alpha

Read more…

Experimenting with transfer learning for visual categorization

DOI

Hi! I am Jean-Nicolas Jérémie and the goal of this notebook is to provide a framework to implement (and experiment with) transfer learning on deep convolutional neuronal network (DCNN). In a nutshell, transfer learning allows to re-use the knowlegde learned on a problem, such as categorizing images from a large dataset, and apply it to a different (yet related) problem, performing the categorization on a smaller dataset. It is a powerful method as it allows to implement complex task de novo quite rapidly (in a few hours) without having to retrain the millions of parameters of a DCNN (which takes days of computations). The basic hypothesis is that it suffices to re-train the last classification layers (the head) while keeping the first layers fixed. Here, these networks teach us also some interesting insights into how living systems may perform such categorization tasks.

Based on our previous work, we will start from a VGG16 network loaded from the torchvision.models library and pre-trained on the Imagenet dataset wich allows to perform label detection on naturals images for $K = 1000$ labels. Our goal here will be to re-train the last fully-Connected layer of the network to perfom the same task but in a sub-set of $K = 10$ labels from the Imagenet dataset.

Moreover, we are going to evaluate different strategies of transfer learning:

  • VGG General : Substitute the last layer of the pyTorch VGG16 network ($K = 1000$ labels) with a new layer build from a specific subset ($K = 10$ labels).
  • VGG Linear : Add a new layer build from a specific subset ($K = 10$ labels) after the last Fully-Connected layer of the the pyTorch VGG16 network.
  • VGG Gray : Same architecture as the VGG General network but trained with grayscale images.
  • VGG Scale : Same architecture as the VGG General network but trained with images of different size.
  • VGG Full : Same architecture as the VGG General network but all the layers are trained (otherwise I trained the last Fully-Connected layer).

In this notebook, I will use the pyTorch library for running the networks and the pandas library to collect and display the results. This notebook was done during a master 2 internship at the Neurosciences Institute of Timone (INT) under the supervision of Laurent Perrinet. It is curated in the following github repo.

Read more…

Modelling Ocean surface waves

Trying to model Ocean surface waves, I have played using a linear superposition of sinusoids and also on the fact that phase speed (following a wave's crest) is twice as fast as group speed (following a group of waves). Finally, I more recently used such generation of a model of the random superposition of waves to model the wigggling lines formed by the refraction (bendings of the trajectory of a ray at the interface between air and water) of light, called caustics...

Observing real-life ocean waves instructed me that if a single wave is well approximated by a sinusoïd, each wave is qualitatively a bit different. Typical for these surface gravity waves are the sharp crests and flat troughs. As a matter of fact, modelling ocean waves is on one side very useful (Ocean dynamics and its impact on climate, modelling tides, tsunamis, diffraction in a bay to predict coastline evolution, ...) but quite demanding despite a well known mathematical model. Starting with the Navier-Stokes equations to an incompressible fluid (water) in a gravitational field leads to Luke's variational principle in certain simplifying conditions. Further simplifications lead to the approximate solution given by Stokes which gives the following shape as the sum of different harmonics:

Stokes wave(https://en.wikipedia.org/wiki/Stokes_wave)

This seems well enough at the moment and I will capture this shape in this notebook and notably if that applies to a random mixture of such waves...

(WORK IN PROGRESS)

The current situation is that these solutions seem to not fit what is displayed on the wikipedia page and that I do not spot the bug I may have introduced... More work on this is needed and any feedback is welcome...

Read more…

Density of stars on the surface of the sky

DOI

Looking at the night sky, the pattern of stars on the surface of the sky follows a familiar pattern. The Big Dipper, Cassiopeia, the Pleiades, or Orion are popular landmarks in the sky which we can immediatly recognize.

Different civilisations labelled these patterns using names such as constellations in the western world. However, this pattern is often the result of pure chance. Stars from one constellation belong often to remote areas in the universe and they bear this familiarity only because we always saw them as such; the rate at which stars move is much shorter than the lifespan of humanity.

I am curious here to study the density of stars as they appear on the surface of the sky. It is both a simple question yet a complex to formulate. Is there any generic principle that could be used to characterize their distribution? This is my attempt to answer the question

https://astronomy.stackexchange.com/questions/43147/density-of-stars-on-the-surface-of-the-sky

(but also to make the formulation of the question clearer...). This is my answer:

Read more…

Fitting COVID data

I propose here a simple method to fit experimental data common to epidemiological spreads, such as the present COVID-19 pandemic, using the inverse gaussian distribution. This follows the general incompregension of my answer to the question Is the COVID-19 pandemic curve a Gaussian curve? on StackOverflow. My initial point is to say that a Gaussian is not adapted as it handles a distribution on real numbers, while such a curve (the variable being number of days) handles numbers on the half line. Inspired by the excellent A Theory of Reaction Time Distributions by Dr Fermin Moscoso del Prado Martin a constructive approach is to propose another distribution, such as the inverse Gaussian distribution.

This notebook develops this same idea on real data and proves numerically how bad the Gaussian fit is compared to the latter. Thinking about the importance of doing a proper inference in such a case, I conclude

Read more…

Benchmarking CNNs

Hi! I am Jean-Nicolas Jérémie and the goal of this benchmark is to offer a comparison between differents pre-trained image recognition's networks based on the Imagenet dataset wich allows to work on naturals images for $1000$ labels. These different networks tested here are taken from the torchvision.models library : AlexNet, VGG16, MobileNetV2 and ResNet101.

Our use case is to measure the performance of a system which receives a sequence of images and has to make a decision as soon as possible, hence with batch_size=1. Specifically, we wish also to compare different computing architectures such as CPUs, desktop GPUs or other more exotic platform such as the Jetson TX2 (experiment 1). Additionally, we will implement some image transformations as up/down-sampling (experiment 2) or transforming to grayscale (experiment 3) to quantify their influence on the accuracy and computation time of each network.

In this notebook, I will use the Pytorch library for running the networks and the pandas library to collect and display the results. This notebook was done during a master 1 internship at the Neurosciences Institute of Timone (INT) under the supervision of Laurent PERRINET. It is curated in the following github repo.

Read more…

nesting jupyter runs

Jupyter notebooks are a great way of sharing knowledge in science, art, programming. For instance, in a recent musing, I tried to programmatically determine the color of the sky. This renders as a web page, but is also a piece of runnable code.

As such, they are also great ways to store the knowledge that was acquired at a given time and that could be reusable. This may be considered as bad programming and may have downsides as described in that slides :

Joel Grus

Recently, thanks to an answer to a stack overflow question, I found a way to overcome this by detecting if the caall to a notebook is made from the notebook itself or from a parent.

Read more…

Colors of the sky

Our sensorial environment contains multiple regularities which our brain uses to optimize its representation of the world: objects fall most of the time downwards, the nose is usually in the middle below the eyes, the sky is blue... Concerning this last point, I wish here to illustrate the physical origins of this phenomenon and in particular the range of colors that you may observe in the sky.

Read more…

Caustic (optics)

Caustics (wikipedia are luminous patterns which are resulting from the superposition of smoothly deviated light rays. It is for instance the heart-shaped pattern in your cup of coffee which is formed as the rays of the sun are reflected on the cup's surface. It is also the wiggly pattern of light curves that you will see on the floor of a pool as the sun's light is refracted at the surface of the water. Here, we simulate that particular physical phenomenon. Simply because they are mesmerizingly beautiful, but also as it is of interest in visual neuroscience. Indeed, it speaks to how images are formed (more on this later), hence how the brain may understand images.

In this post, I will develop a simple formalism to generate such patterns, with the paradoxical result that it is very simple to code yet generates patterns with great complexity, such as:



This is joint work with artist Etienne Rey, in which I especially follow the ideas put forward in the series Turbulence.

DOI

Read more…

Fitting a psychometric curve using pyTorch

The goal here is to compare methods which fit data with psychometric curves using logistic regression. Indeed, after (long) experiments where for instance you collected sequences of keypresses, it is important to infer at best the parameters of the underlying processes: was the observer biased, or more precise?

While I was forevever using sklearn or lmfit (that is, scipy's minimize) and praised these beautifully crafted methods, I sometimes lacked some flexibility in the definition of the model. This notebook was done in collaboration with Jenna Fradin, master student in the lab.

tl; dr = Do not trust the coefficients extracted by a fit without validating for methodological biases.

One part of flexibility I missed is taking care of the lapse rate, that is the frequency with which you just miss the key. In a psychology experiment, you often see a fast sequence of trials for which you have to make a perceptual deccision, for instance press the Left or Right arrows. Sometimes you know the answer you should have done, but press the wrong eror. This error of distraction is always low (in the order of 5% to 10%) but could potentially change the results of the experiments. This is one of the aspects we will evaluate here.

In this notebook, I define a fitting method using pytorch which fits in a few lines of code :

In [1]:
import torch
from torch.utils.data import TensorDataset, DataLoader

torch.set_default_tensor_type("torch.DoubleTensor")
criterion = torch.nn.BCELoss(reduction="sum")

class LogisticRegressionModel(torch.nn.Module):
    def __init__(self, bias=True, logit0=-2, theta0=0, log_wt=torch.log(0.1*torch.ones(1))):
        super(LogisticRegressionModel, self).__init__()
        #self.linear = torch.nn.Linear(1, 1, bias=bias)
        self.theta0 = torch.nn.Parameter(theta0 * torch.ones(1))
        self.logit0 = torch.nn.Parameter(logit0 * torch.ones(1))
        self.log_wt = torch.nn.Parameter(log_wt * torch.ones(1))

    def forward(self, theta):
        p0 = torch.sigmoid(self.logit0)
        #out = p0 / 2 + (1 - p0) * torch.sigmoid(self.linear(theta))
        out = p0 / 2 + (1 - p0) * torch.sigmoid((theta-self.theta0 )/torch.exp(self.log_wt))
        return out

learning_rate = 0.005
beta1, beta2 = 0.9, 0.999
betas = (beta1, beta2)
num_epochs = 2 ** 9 + 1
batch_size = 256
amsgrad = False # gives similar results
amsgrad = True  # gives similar results

def fit_data(
    theta,
    y,
    learning_rate=learning_rate,
    batch_size=batch_size,  # gamma=gamma,
    num_epochs=num_epochs,
    betas=betas,
    verbose=False, **kwargs
):

    Theta, labels = torch.Tensor(theta[:, None]), torch.Tensor(y[:, None])
    loader = DataLoader(
        TensorDataset(Theta, labels), batch_size=batch_size, shuffle=True
    )

    device = torch.device("cuda" if torch.cuda.is_available() else "cpu")

    logistic_model = LogisticRegressionModel()
    logistic_model = logistic_model.to(device)
    logistic_model.train()
    optimizer = torch.optim.Adam(
        logistic_model.parameters(), lr=learning_rate, betas=betas, amsgrad=amsgrad
    )
    for epoch in range(int(num_epochs)):
        logistic_model.train()
        losses = []
        for Theta_, labels_ in loader:
            Theta_, labels_ = Theta_.to(device), labels_.to(device)
            outputs = logistic_model(Theta_)
            loss = criterion(outputs, labels_)

            optimizer.zero_grad()
            loss.backward()
            optimizer.step()
            losses.append(loss.item())

        if verbose and (epoch % (num_epochs // 32) == 0):
            print(f"Iteration: {epoch} - Loss: {np.sum(losses)/len(theta):.5f}")

    logistic_model.eval()
    Theta, labels = torch.Tensor(theta[:, None]), torch.Tensor(y[:, None])
    outputs = logistic_model(Theta)
    loss = criterion(outputs, labels).item() / len(theta)
    return logistic_model, loss

and run a series of tests to compare both methods.

Read more…

Role of gamma correction in Sparse coding

I have previously shown a python implementation which allows for the extraction a sparse set of edges from an image. We were using the raw luminance as the input to the algorithm. What happens if you use gamma correction?

albert on gamma

  • Results : for this particular image, we checked that using the luminance ($\gamma \approx 1$) is the correct choice. The outcome is that gamma correction may improve coding, but only slightly. In the figure below, we plot as a function of gamma the final energy of the error and the perceptually relevant measure of structural simailarity :

albert on gamma

@inbook{Perrinet15bicv,
    title = {Sparse models},
    author = {Perrinet, Laurent U.},
    booktitle = {Biologically-inspired Computer Vision},
    chapter = {13},
    editor = {Keil, Matthias and Crist\'{o}bal, Gabriel and Perrinet, Laurent U.},
    publisher = {Wiley, New-York},
    year = {2015}
}

Read more…

Sparse coding of large images

In this post we would try to show how one could infer the sparse representation of an image knowing an appropriate generative model for its synthesis. We will start by a linear inversion (pseudo-inverse deconvolution), and then move to a gradient descent algorithm. Finally, we will implement a convolutional version of the iterative shrinkage thresholding algorithm (ISTA) and its fast version, the FISTA.

For computational efficiency, all convolutions will be implemented by a Fast Fourier Tansform, so that a standard convolution will be mathematically exactly similar. We will benchmark this on a realistic image size of $512 \times 512$ giving some timing results on a standard laptop.

Read more…

Feature vs global motion

As we see a visual scene, there is contribution of the motion of each of the objects that constitute the visual scene into detecting its global motion. In particular, it is debatable to know which weight individual features, such as small objects in the foreground, have into this computation compared to a dense texture-like stimulus, as that of the background for instance.

Here, we design a a stimulus where we control independently these two aspects of motions to titrate their relative contribution to the detection of motion.

Can you spot the motion ? Is it more going to the upper left or to the upper right?

(For a more controlled test, imagine you fixate on the center of the movie.)

Read more…

Embedding a trajectory in noise

Motion detection has many functions, one of which is the potential localization of the biomimetic camouflage seen in this video. Can we test this in the lab by using synthetic textures such as MotionClouds?

However, by construction, MotionClouds have no spatial structure and it seems interesting to consider more complex trajectories. Following a previous post, we design a trajectory embedded in noise.

Can you spot the motion ? from left to right or reversed ?

(For a more controlled test, imagine you fixate on the top left corner of each movie.)

(Upper row is coherent, lower row uncoherent / Left is -> Right column is <-)

Read more…

Rainbow effect

When I see a rainbow, I perceive the luminance inside the arc to be brighter than outside the arc. Is this effect percpetual (inside our head) or physical (inside each droplet in the sky). So, this is a simple notebook to show off how to synthesize the image of a rainbow on a realistic sky. TL;DR: there must be a physical reason for it.

Outline: The rainbow is a set of colors over a gradient of hues, masked for certain ones. The sky will be a gradient over blueish colors.

Read more…

Statistics of the natural input to a ring model

What does the input to a population of neurons in the primary visual cortex look like? In this post, we will try to have a feeling of the structure and statistics of the natural input to such a "ring" model.

This notebook explores this question using a retina-like temporal filtering and oriented Gabor-like filters. It produces this polar plot of the instantaneous energy in the different orientations for a natural movie :



One observes different striking features in the structure of this input to populations of V1 neurons:

  • input is sparse: often, a few orientations dominate - the shape of these components (bandwidth) seem to be similar,
  • there are many "switches": at some moments, the representations flips to another. This is due to cuts in the movie (changes from one scene to the other for instance). In a more realistic setting where we would add eye movements, these switches should also happen during saccades (but is there any knowledge of the occurence of the switch by the visual system?),
  • between switches, there is some coherence in amplitude (a component will slowly change its energy) but also in time (a component is more likely to have a ghradually changing oriantation, for instance when the scene rotates).

This structure is specific to the structure of natural images and to the way they transform (translations, rotations, zooms due to the motion and deformation of visual objects). This is certainly incorporated as a "prior" information in the structure of the visual cortex. As to know how and where this is implemented is an open scientific question.

This is joint work with Hugo Ladret.

Read more…

Extending datasets in pyTorch

PyTorch is a great library for machine learning. You can in a few lines of codes retrieve a dataset, define your model, add a cost function and then train your model. It's quite magic to copy and paste code from the internet and get the LeNet network working in a few seconds to achieve more than 98% accuracy.

However, it can be tedious sometimes to extend existing objects and here, I will manipulate some ways to define the right dataset for your application. In particular I will modify the call to a standard dataset (MNIST) to place the characters at random places in a large image.

Read more…

Predictive coding of variable motion

In some recent modeling work:

Laurent Perrinet, Guillaume S. Masson. Motion-based prediction is sufficient to solve the aperture problem. Neural Computation, 24(10):2726--50, 2012 https://laurentperrinet.github.io/publication/perrinet-12-pred

we study the role of transport in modifying our perception of motion. Here, we test what happens when we change the amount of noise in the stimulus.

In this script the predictive coding is done using the MotionParticles package and for a motion texture within a disk aperture.

Read more…

accessing the data from a pupil recording

I am experimenting with the pupil eyetracker and could set it up (almost) smoothly on a macOS. There is an excellent documentation, and my first goal was to just record raw data and extract eye position.

In [1]:
from IPython.display import HTML
HTML('<center><video controls autoplay loop src="https://laurentperrinet.github.io/sciblog/files/2017-12-13_pupil%20test_480.mp4" width=61.8%/></center>')
Out[1]:

This video shows the world view (cranio-centric, from a head-mounted camera fixed on the frame) with overlaid the position of the (right) eye while I am configuring a text box. You see the eye fixating on the screen then jumping somewhere else on the screen (saccades) or on the keyboard / hands. Note that the screen itself shows the world view, such that this generates an self-reccurrent pattern.

For this, I could use the capture script and I will demonstrate here how to extract the raw data in a few lines of python code.

Read more…

Computing sparseness of natural images with retina-like RFs

In [1]:
%load_ext autoreload
%autoreload 2

SparseEdges : computing sparseness of natural images with retina-like RFs

Let's compute the "edges" produced with symmetrical filters.

Initialization

defining framework

In [2]:
from __future__ import division, print_function
pltimport numpy as np
np.set_printoptions(precision=2, suppress=True)

cluster = False

experiment = 'retina-sparseness'
name_database = 'serre07_distractors'
#parameter_file = '/Users/laurentperrinet/pool/science/BICV/SparseEdges/default_param.py'
parameter_file = 'https://raw.githubusercontent.com/bicv/SparseEdges/master/default_param.py'
#lena_file = '/Users/laurentperrinet/pool/science/BICV/SparseEdges//database/lena256.png'
lena_file = 'https://raw.githubusercontent.com/bicv/SparseEdges/master/database/lena256.png'
lena_file = '../../BICV/SparseEdges/database/lena256.png'
N_image = 100
N = 2**11
B_theta = np.inf
do_linear = False
In [3]:
from SparseEdges import SparseEdges
mp = SparseEdges(parameter_file)
mp.pe.N_X, mp.pe.N_Y = 64, 64
mp.pe.figpath, mp.pe.formats, mp.pe.dpi = 'figures', ['png', 'pdf', 'jpg'], 450
mp.init()
print ('Range of spatial frequencies: ', mp.sf_0)

Range of spatial frequencies:  [ 0.62  0.38  0.24  0.15  0.09  0.06  0.03  0.02]
In [4]:
mp.pe
Out[4]:
{'B_sf': 0.4,
 'B_theta': 0.17453277777777776,
 'C_range_begin': -5,
 'C_range_end': 10.0,
 'MP_alpha': 0.7,
 'MP_do_mask': True,
 'MP_rho': None,
 'N': 2048,
 'N_Dtheta': 24,
 'N_X': 64,
 'N_Y': 64,
 'N_image': None,
 'N_phi': 12,
 'N_r': 6,
 'N_scale': 5,
 'N_svm_cv': 50,
 'N_svm_grid': 32,
 'base_levels': 1.618,
 'd_max': 2.0,
 'd_min': 0.5,
 'd_width': 45.0,
 'datapath': 'database',
 'dip_B_psi': 0.1,
 'dip_B_theta': 1.0,
 'dip_epsilon': 0.5,
 'dip_scale': 1.5,
 'dip_w': 0.2,
 'do_edgedir': False,
 'do_mask': True,
 'do_rank': False,
 'do_whitening': True,
 'dpi': 450,
 'edge_mask': True,
 'edge_scale_chevrons': 180.0,
 'edgefigpath': 'results/edges',
 'edgematpath': 'data_cache/edges',
 'eta_SO': 0.0,
 'figpath': 'figures',
 'figsize': 14.0,
 'figsize_cohist': 8,
 'figsize_hist': 8,
 'formats': ['png', 'pdf', 'jpg'],
 'gamma_range_begin': -14,
 'gamma_range_end': 3,
 'kappa_phase': 0.0,
 'line_width': 1.0,
 'line_width_chevrons': 0.75,
 'loglevel_max': 7,
 'mask_exponent': 3.0,
 'matpath': 'data_cache',
 'multiscale': True,
 'n_theta': 24,
 'noise': 0.33,
 'scale': 0.8,
 'scale_chevrons': 2.5,
 'scale_circle': 0.08,
 'scale_invariant': True,
 'seed': 42,
 'svm_KL_m': 0.34,
 'svm_log': False,
 'svm_max_iter': -1,
 'svm_n_jobs': 1,
 'svm_norm': False,
 'svm_test_size': 0.2,
 'svm_tol': 0.001,
 'verbose': 30,
 'weight_by_distance': True,
 'white_N': 0.07,
 'white_N_0': 0.0,
 'white_alpha': 1.4,
 'white_f_0': 0.4,
 'white_n_learning': 0,
 'white_name_database': 'serre07_distractors',
 'white_recompute': False,
 'white_steepness': 4.0}
In [2]:
import matplotlib
pylab_defaults = { 
    'font.size': 10,
    'xtick.labelsize':'medium',
    'ytick.labelsize':'medium',
    'text.usetex': False,
    'font.family' : 'sans-serif',
    'font.sans-serif' : ['Helvetica'],
    }
matplotlib.rcParams.update(pylab_defaults)

%matplotlib inline
import matplotlib.pyplot as plt
%config InlineBackend.figure_format='retina'
#%config InlineBackend.figure_format = 'svg'
fig_width_pt = 397.48  # Get this from LaTeX using \showthe\columnwidth
inches_per_pt = 1.0/72.27               # Convert pt to inches
fig_width = fig_width_pt*inches_per_pt  # width in inches
#fig_width = 21
figsize=(fig_width, .618*fig_width)
#figpath, ext = os.path.join(os.getenv('HOME'), 'pool/science/RetinaClouds/2016-05-20_nips'), '.pdf'

Standard edges are oriented, but one may modify that:

In [6]:
sf_0 = .09 # TODO .1 cycle / pixel (Geisler)
params= {'sf_0':sf_0, 'B_sf': mp.pe.B_sf, 'theta':np.pi, 'B_theta': mp.pe.B_theta}
FT_lg = mp.loggabor(mp.pe.N_X/2, mp.pe.N_Y/2, **params)
#(fourier_domain(mp.normalize(np.absolute(FT_lg), center=False))+ image_domain(mp.normalize(mp.invert(FT_lg), center=False)))
fig, a1, a2 = mp.show_FT(FT_lg, axis=True, figsize=(fig_width, fig_width/2))
fig.tight_layout()
mp.savefig(fig, experiment + '_loggabor')
In [7]:
sf_0 = .06 # TODO .1 cycle / pixel (Geisler)
params= {'sf_0':sf_0, 'B_sf': mp.pe.B_sf, 'theta':0., 'B_theta': np.inf}
FT_lg = mp.loggabor(mp.pe.N_X/2, mp.pe.N_Y/2, **params)
fig, a1, a2 = mp.show_FT(FT_lg, axis=True, figsize=(fig_width, fig_width/2))
fig.tight_layout()
mp.savefig(fig, experiment + '_dog')

When defining the framework, one thus needs only one angle:

In [8]:
print ('Range of angles (in degrees): ', mp.theta*180./np.pi)
mp.pe.n_theta = 1
mp.pe.B_theta = np.inf
mp.init()
print ('Range of angles (in degrees): ', mp.theta*180./np.pi)

Range of angles (in degrees):  [-82.5 -75.  -67.5 -60.  -52.5 -45.  -37.5 -30.  -22.5 -15.   -7.5   0.
   7.5  15.   22.5  30.   37.5  45.   52.5  60.   67.5  75.   82.5  90. ]
Range of angles (in degrees):  [ 90.]
In [9]:
print('Final sparseness in the representation = {}'.format(mp.pe.N/mp.oc))
print('Final sparseness in the pyramid = {}'.format(mp.pe.N/(4/3*mp.pe.N_X*mp.pe.N_Y)))

Final sparseness in the representation = 0.0625
Final sparseness in the pyramid = 0.375

one example image

In [10]:
mp = SparseEdges(parameter_file)
mp.pe.figpath, mp.pe.formats, mp.pe.dpi = 'figures', ['png', 'pdf', 'jpg'], 450

image = mp.imread(lena_file)
mp.pe.N = N
mp.pe.do_mask = True
mp.pe.n_theta = 1
mp.pe.B_theta = B_theta
mp.pe.line_width = 0
mp.pe.mask_exponent = 4.
mp.init()
image = mp.normalize(image, center=False)
image *= mp.mask
print(image.min(), image.max())
fig, ax = mp.imshow(image, mask=True, norm=False)

-0.950759120364 0.891900615494
In [11]:
name = experiment.replace('sparseness', 'lena')
matname = os.path.join(mp.pe.matpath, name + '.npy')
try:
    edges = np.load(matname)
except:
    edges, C_res = mp.run_mp(image, verbose=False)
    np.save(matname, edges)    

    
matname = os.path.join(mp.pe.matpath, name + '_rec.npy')
try:
    image_rec = np.load(matname)
except:
    image_rec = mp.reconstruct(edges, mask=True)        
    np.save(matname, image_rec)
In [12]:
print(matname)

data_cache/retina-lena_rec.npy
In [13]:
#mp.pe.line_width = 0
fig, a = mp.show_edges(edges, image=mp.dewhitening(image_rec), show_phase=False, mask=True)
mp.savefig(fig, name)