A bit more fun with gravity waves
More fun with gravity waves¶
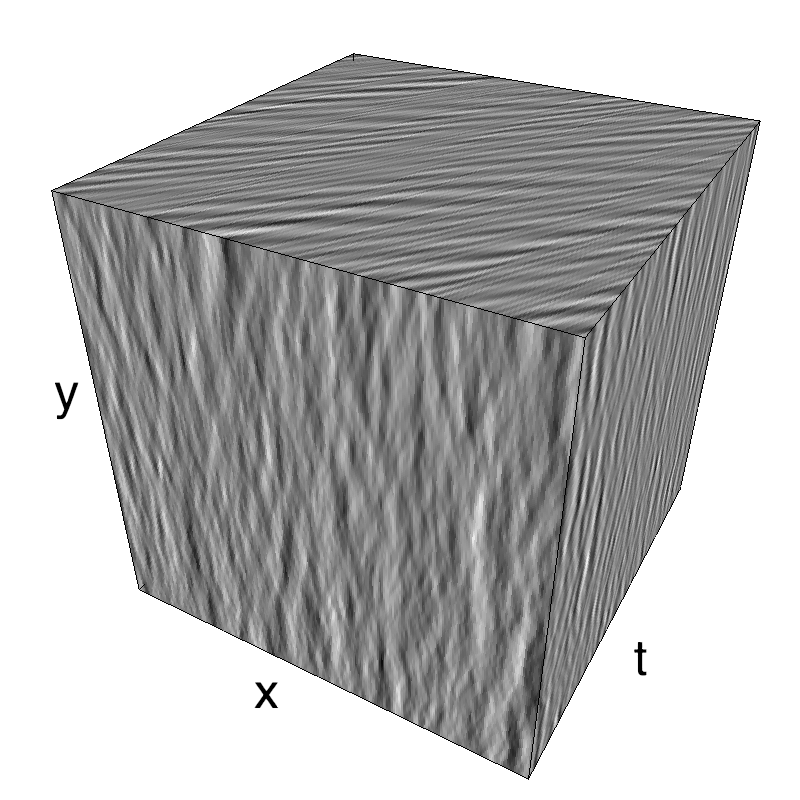
Motion Clouds were defined in the origin to provide a simple parameterization for textures. Thus we used a simple unimodal, normal distribution (on the log-radial frequency space to be more precise). But the larger set of Random Phase Textures may provide some interesting examples, some of them can even be fun! This is the case of this simulation of the waves you may observe on the surface on the ocean.
Main features of gravitational waves are:
- longer waves travel faster (tsunami are fast and global, ripples are slow and local) - speed is linearly proportional to wavelength
- phase speed (following a wave's crest) is twice as fast as group speed (following a group of waves).
More info about deep water waves : http://farside.ph.utexas.edu/teaching/336L/Fluidhtml/node122.html
In [1]:
import os
import numpy as np
import MotionClouds as mc
fx, fy, ft = mc.get_grids(mc.N_X, mc.N_Y, mc.N_frame)
mc.figpath = '../files/2016-04-24_a-wave-going-backwards'
if not(os.path.isdir(mc.figpath)): os.mkdir(mc.figpath)
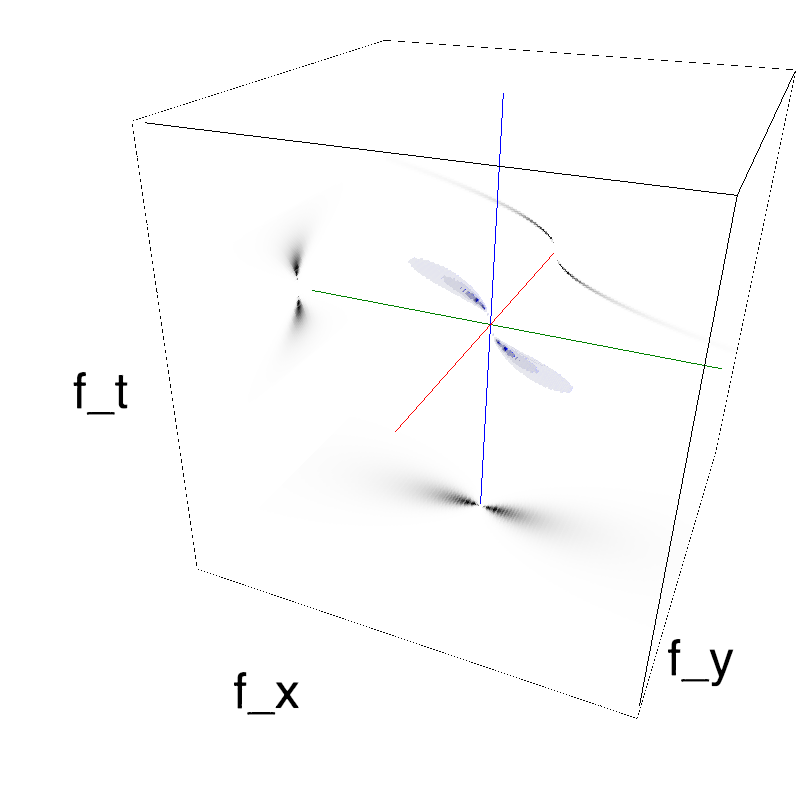
def envelope_gravity(fx, fy, ft, B_wave, V_X, V_Y, g=.1):
"""
Gravitational envelope:
selects the manifold corresponding to the speed (V_X, V_Y) with some thickness B_V
"""
k = fx*V_X+fy*V_Y
env = np.exp(-.5*(((ft/.5)**2-g*np.sqrt(((k/.5)**2)))**2/(B_wave*mc.frequency_radius(fx, fy, ft, clean_division=True))**2))
env *= (ft*k) < 0
return env
def envelope_gabor_wave(fx, fy, ft, B_wave, V_X, V_Y,
B_V=mc.B_V, B_v=1., sf_0=mc.sf_0, B_sf=mc.B_sf, loggabor=mc.loggabor,
theta=mc.theta, B_theta=mc.B_theta, alpha=mc.alpha):
"""
Returns the Motion Cloud kernel
"""
envelope = mc.envelope_gabor(fx, fy, ft, V_X, V_Y,
B_V=B_V, sf_0=sf_0, B_sf=B_sf, loggabor=loggabor,
theta=theta, B_theta=B_theta, alpha=alpha)
envelope *= envelope_gravity(fx, fy, ft, B_wave=B_wave, V_X=V_X, V_Y=V_Y)
return envelope
In [2]:
name = 'wave2'
theta, B_theta, B_wave = 0., np.pi/12., .02
alpha, sf_0, B_sf, B_V = 1., .2, .4, 2.
recompute = True
env = envelope_gabor_wave(fx, fy, ft, V_X=1.5, V_Y=0., B_wave=B_wave, B_V=B_V,
theta=theta, B_theta=B_theta, sf_0=sf_0, B_sf=B_sf, alpha=alpha)
mc.figures(env, name, recompute=recompute, figpath=mc.figpath)
mc.in_show_video(name, figpath=mc.figpath)
In [3]:
name = 'wave2_back'
im = mc.rectif(mc.random_cloud(env))
In [4]:
im_back = im.copy()
for i in range(mc.N_frame):
im_back[:, :, i] = np.roll(im[:, :, i], -i, axis=0)
mc.anim_save(im_back, os.path.join(mc.figpath, name))
mc.in_show_video(name, figpath=mc.figpath)
Post-prod¶
In [5]:
!curl https://upload.wikimedia.org/wikipedia/commons/thumb/4/4f/Paperboat.svg/1000px-Paperboat.svg.png -o /tmp/Paperboat.png
In [6]:
# Import everything needed to edit video clips
import moviepy.editor as mvp
w,h = moviesize = (mc.N_X, mc.N_Y)
fps = 25
zoom = 1.5
duration = mc.N_frame/fps
clip = mvp.VideoFileClip(os.path.join(mc.figpath, name+mc.vext))
clip.ipython_display(fps=fps, duration=duration, autoplay=1, loop=1)
Out[6]:
In [7]:
overlay = mvp.ImageClip('/tmp/Paperboat.png').resize((zoom*mc.N_X/3, zoom*mc.N_Y/4))
overlay.duration = clip.duration
overlay.ipython_display(duration=duration, autoplay=1, loop=1)
Out[7]:
In [8]:
#overlay.rotate(lambda t:10*np.sin(2*np.pi*t/duration))
#overlay.fl_time(mvp.vfx.rotate, lambda t:10*np.sin(2*np.pi*t/duration))
overlay = overlay.fx(mvp.vfx.rotate, lambda t:10*np.sin(2*np.pi*t/duration))
overlay = overlay.set_position((mc.N_X/2-zoom*mc.N_X/6, mc.N_Y/2-zoom*mc.N_Y/8))
final_clip = mvp.CompositeVideoClip([clip, overlay])
final_clip.duration = duration
final_clip.ipython_display(fps=fps, duration=duration, autoplay=1, loop=1)
Out[8]:
In [9]:
final_clip.write_videofile("/tmp/moving_backwards.mp4", fps=fps)
some book keeping for the notebook¶
In [1]:
%load_ext version_information
%version_information numpy, scipy, matplotlib, MotionClouds
Out[1]: