Computing sparseness of natural images with retina-like RFs

Laurent Perrinet

2017-11-21 11:56

In [1]:

%load_ext autoreload
%autoreload 2

SparseEdges : computing sparseness of natural images with retina-like RFs¶

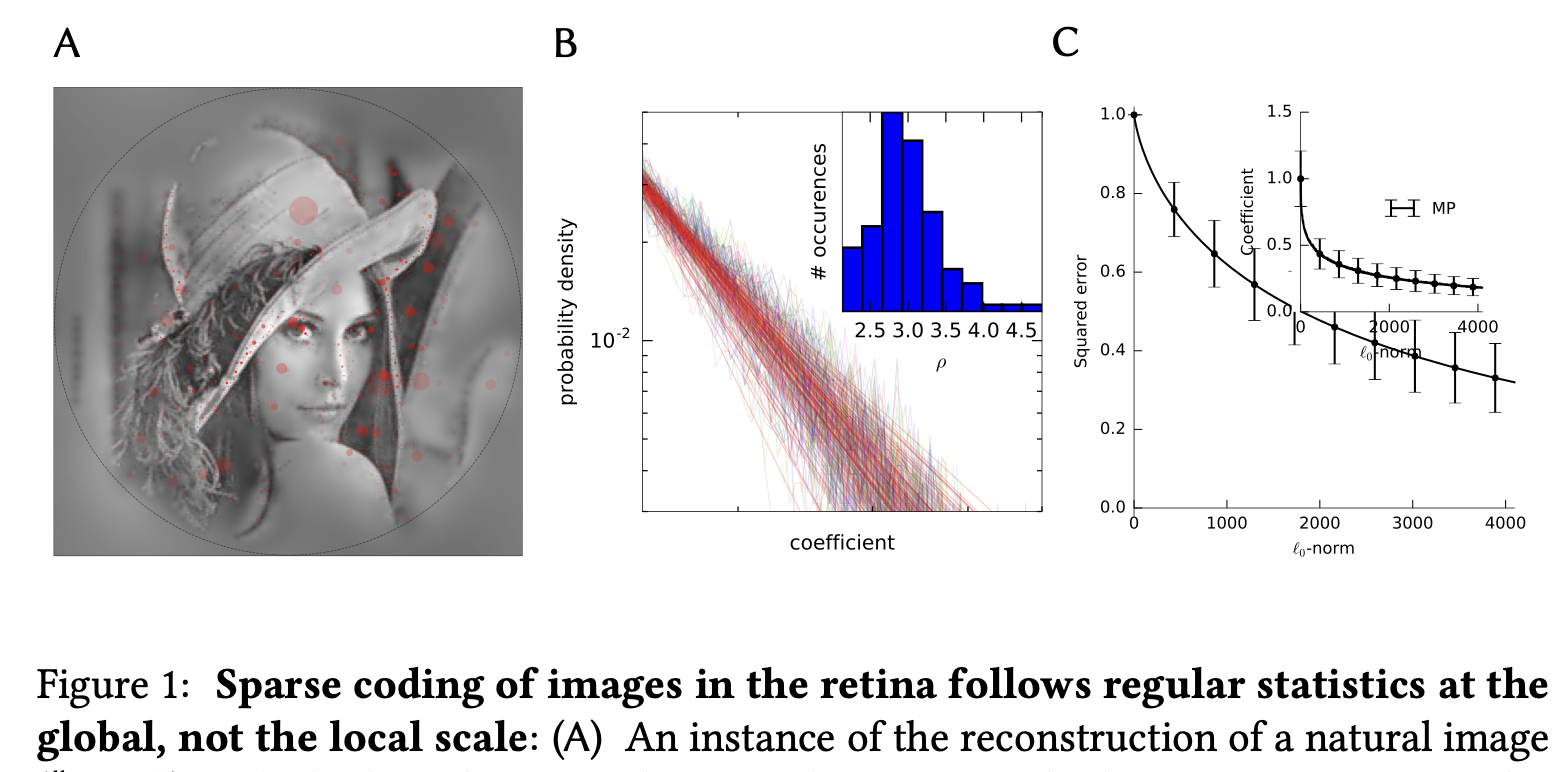
Let's compute the "edges" produced with symmetrical filters.

Initialization¶

defining framework

In [2]:

from __future__ import division, print_function
pltimport numpy as np
np.set_printoptions(precision=2, suppress=True)

cluster = False

experiment = 'retina-sparseness'
name_database = 'serre07_distractors'
#parameter_file = '/Users/laurentperrinet/pool/science/BICV/SparseEdges/default_param.py'
parameter_file = 'https://raw.githubusercontent.com/bicv/SparseEdges/master/default_param.py'
#lena_file = '/Users/laurentperrinet/pool/science/BICV/SparseEdges//database/lena256.png'
lena_file = 'https://raw.githubusercontent.com/bicv/SparseEdges/master/database/lena256.png'
lena_file = '../../BICV/SparseEdges/database/lena256.png'
N_image = 100
N = 2**11
B_theta = np.inf
do_linear = False

In [3]:

from SparseEdges import SparseEdges
mp = SparseEdges(parameter_file)
mp.pe.N_X, mp.pe.N_Y = 64, 64
mp.pe.figpath, mp.pe.formats, mp.pe.dpi = 'figures', ['png', 'pdf', 'jpg'], 450
mp.init()
print ('Range of spatial frequencies: ', mp.sf_0)

Range of spatial frequencies:  [ 0.62  0.38  0.24  0.15  0.09  0.06  0.03  0.02]

In [4]:

mp.pe

Out[4]:

{'B_sf': 0.4,
 'B_theta': 0.17453277777777776,
 'C_range_begin': -5,
 'C_range_end': 10.0,
 'MP_alpha': 0.7,
 'MP_do_mask': True,
 'MP_rho': None,
 'N': 2048,
 'N_Dtheta': 24,
 'N_X': 64,
 'N_Y': 64,
 'N_image': None,
 'N_phi': 12,
 'N_r': 6,
 'N_scale': 5,
 'N_svm_cv': 50,
 'N_svm_grid': 32,
 'base_levels': 1.618,
 'd_max': 2.0,
 'd_min': 0.5,
 'd_width': 45.0,
 'datapath': 'database',
 'dip_B_psi': 0.1,
 'dip_B_theta': 1.0,
 'dip_epsilon': 0.5,
 'dip_scale': 1.5,
 'dip_w': 0.2,
 'do_edgedir': False,
 'do_mask': True,
 'do_rank': False,
 'do_whitening': True,
 'dpi': 450,
 'edge_mask': True,
 'edge_scale_chevrons': 180.0,
 'edgefigpath': 'results/edges',
 'edgematpath': 'data_cache/edges',
 'eta_SO': 0.0,
 'figpath': 'figures',
 'figsize': 14.0,
 'figsize_cohist': 8,
 'figsize_hist': 8,
 'formats': ['png', 'pdf', 'jpg'],
 'gamma_range_begin': -14,
 'gamma_range_end': 3,
 'kappa_phase': 0.0,
 'line_width': 1.0,
 'line_width_chevrons': 0.75,
 'loglevel_max': 7,
 'mask_exponent': 3.0,
 'matpath': 'data_cache',
 'multiscale': True,
 'n_theta': 24,
 'noise': 0.33,
 'scale': 0.8,
 'scale_chevrons': 2.5,
 'scale_circle': 0.08,
 'scale_invariant': True,
 'seed': 42,
 'svm_KL_m': 0.34,
 'svm_log': False,
 'svm_max_iter': -1,
 'svm_n_jobs': 1,
 'svm_norm': False,
 'svm_test_size': 0.2,
 'svm_tol': 0.001,
 'verbose': 30,
 'weight_by_distance': True,
 'white_N': 0.07,
 'white_N_0': 0.0,
 'white_alpha': 1.4,
 'white_f_0': 0.4,
 'white_n_learning': 0,
 'white_name_database': 'serre07_distractors',
 'white_recompute': False,
 'white_steepness': 4.0}

In [2]:

import matplotlib
pylab_defaults = { 
    'font.size': 10,
    'xtick.labelsize':'medium',
    'ytick.labelsize':'medium',
    'text.usetex': False,
    'font.family' : 'sans-serif',
    'font.sans-serif' : ['Helvetica'],
    }
matplotlib.rcParams.update(pylab_defaults)

%matplotlib inline
import matplotlib.pyplot as plt
%config InlineBackend.figure_format='retina'
#%config InlineBackend.figure_format = 'svg'
fig_width_pt = 397.48  # Get this from LaTeX using \showthe\columnwidth
inches_per_pt = 1.0/72.27               # Convert pt to inches
fig_width = fig_width_pt*inches_per_pt  # width in inches
#fig_width = 21
figsize=(fig_width, .618*fig_width)
#figpath, ext = os.path.join(os.getenv('HOME'), 'pool/science/RetinaClouds/2016-05-20_nips'), '.pdf'

Standard edges are oriented, but one may modify that:

In [6]:

sf_0 = .09 # TODO .1 cycle / pixel (Geisler)
params= {'sf_0':sf_0, 'B_sf': mp.pe.B_sf, 'theta':np.pi, 'B_theta': mp.pe.B_theta}
FT_lg = mp.loggabor(mp.pe.N_X/2, mp.pe.N_Y/2, **params)
#(fourier_domain(mp.normalize(np.absolute(FT_lg), center=False))+ image_domain(mp.normalize(mp.invert(FT_lg), center=False)))
fig, a1, a2 = mp.show_FT(FT_lg, axis=True, figsize=(fig_width, fig_width/2))
fig.tight_layout()
mp.savefig(fig, experiment + '_loggabor')

In [7]:

sf_0 = .06 # TODO .1 cycle / pixel (Geisler)
params= {'sf_0':sf_0, 'B_sf': mp.pe.B_sf, 'theta':0., 'B_theta': np.inf}
FT_lg = mp.loggabor(mp.pe.N_X/2, mp.pe.N_Y/2, **params)
fig, a1, a2 = mp.show_FT(FT_lg, axis=True, figsize=(fig_width, fig_width/2))
fig.tight_layout()
mp.savefig(fig, experiment + '_dog')

When defining the framework, one thus needs only one angle:

In [8]:

print ('Range of angles (in degrees): ', mp.theta*180./np.pi)
mp.pe.n_theta = 1
mp.pe.B_theta = np.inf
mp.init()
print ('Range of angles (in degrees): ', mp.theta*180./np.pi)

Range of angles (in degrees):  [-82.5 -75.  -67.5 -60.  -52.5 -45.  -37.5 -30.  -22.5 -15.   -7.5   0.
   7.5  15.   22.5  30.   37.5  45.   52.5  60.   67.5  75.   82.5  90. ]
Range of angles (in degrees):  [ 90.]

In [9]:

print('Final sparseness in the representation = {}'.format(mp.pe.N/mp.oc))
print('Final sparseness in the pyramid = {}'.format(mp.pe.N/(4/3*mp.pe.N_X*mp.pe.N_Y)))

Final sparseness in the representation = 0.0625
Final sparseness in the pyramid = 0.375

one example image¶

In [10]:

mp = SparseEdges(parameter_file)
mp.pe.figpath, mp.pe.formats, mp.pe.dpi = 'figures', ['png', 'pdf', 'jpg'], 450

image = mp.imread(lena_file)
mp.pe.N = N
mp.pe.do_mask = True
mp.pe.n_theta = 1
mp.pe.B_theta = B_theta
mp.pe.line_width = 0
mp.pe.mask_exponent = 4.
mp.init()
image = mp.normalize(image, center=False)
image *= mp.mask
print(image.min(), image.max())
fig, ax = mp.imshow(image, mask=True, norm=False)

-0.950759120364 0.891900615494

In [11]:

name = experiment.replace('sparseness', 'lena')
matname = os.path.join(mp.pe.matpath, name + '.npy')
try:
    edges = np.load(matname)
except:
    edges, C_res = mp.run_mp(image, verbose=False)
    np.save(matname, edges)    

    
matname = os.path.join(mp.pe.matpath, name + '_rec.npy')
try:
    image_rec = np.load(matname)
except:
    image_rec = mp.reconstruct(edges, mask=True)        
    np.save(matname, image_rec)

In [12]:

print(matname)

data_cache/retina-lena_rec.npy

In [13]:

#mp.pe.line_width = 0
fig, a = mp.show_edges(edges, image=mp.dewhitening(image_rec), show_phase=False, mask=True)
mp.savefig(fig, name)