La vibration des apparences
Laurent Perrinet
Journées d’Ouverture Scientifique (JOS)
[2025-04-18]

“L’irraisonnable efficacité de la vision”
![Comment la vision a évolué... [[Perrinet, 2024]](https://theconversation.com/chats-mouches-humains-comment-la-vision-a-evolue-en-de-multiples-facettes-220083)](https://images.theconversation.com/files/568221/original/file-20240108-17-78s0cj.png)
Illusions visuelles
](https://laurentperrinet.github.io/2022-01-12_NeuroCercle/figures/42_rotsnakes_main.jpg)
Illusions visuelles
Illusions visuelles
Illusions visuelles
Illusions visuelles : Paréidolie
)](https://laurentperrinet.github.io/2022-01-12_NeuroCercle/figures/Face-on-mars.jpg)
Illusions visuelles : Paréidolie
)](https://laurentperrinet.github.io/2022-01-12_NeuroCercle/figures/Viking_moc_face_20m_low.png)
Illusions visuelles : Paréidolie
)](https://laurentperrinet.github.io/2022-01-12_NeuroCercle/figures/Viking_moc_face_20m_high.png)
Neurosciences computationnelles de la vision
]](https://github.com/laurentperrinet/2019-04-03_a_course_on_vision_and_modelization/raw/master/figures/Churchland92.png)
Anatomie du système visuel humain
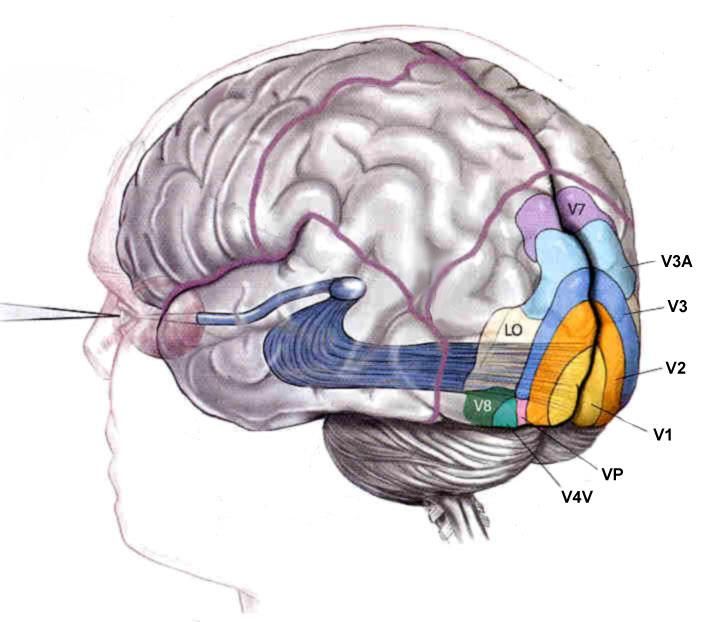
Cortex visuel primaire
![[Hubel & Wiesel, 1962]](https://github.com/laurentperrinet/2019-04-03_a_course_on_vision_and_modelization/raw/master/figures/scientists.jpg)
Cortex visuel primaire
[Hubel & Wiesel, 1962]
Modèles hybrides d’IA
![Using goal-driven deep learning models to understand sensory cortex [Yamins & DiCarlo, 2016]](https://knu-brainai.github.io/images/cnn.png)
Art & Sciences
](https://laurentperrinet.github.io/author/etienne-rey/avatar_hu5659200743397184484.jpg)
](https://ondesparalleles.org/wp-content/uploads/2014/02/cloche_fiche_a.jpg)
Tropique
](https://ondesparalleles.org/wp-content/uploads/2014/02/tropique_fiche_b.jpg)
Tropique
Tropique
](https://ondesparalleles.org/wp-content/uploads/2014/04/etienne_rey_horizons_variables_news2.jpg)
](https://laurentperrinet.github.io/post/2016-06-02_elasticite/TRAME_Elasticit%c3%a9.jpg)
TRAME ÉLASTICITÉ
De la nature des choses
Par Cmglee — Travail personnel, CC BY-SA 4.0, Lien
](https://laurentperrinet.github.io/post/2019-06-22_ardemone/featured.png)
](https://laurentperrinet.github.io/post/2021-10-04_interstices/featured.jpg)
Caustiques

La vibration des apparences
](https://upload.wikimedia.org/wikipedia/commons/c/c9/Montagne_Sainte-Victoire%2C_par_Paul_C%C3%A9zanne_108.jpg)
La vibration des apparences
](https://laurentperrinet.github.io/talk/2025-04-18-vibration-apparences/Merleau-Ponty_Sens-et-non-sens.png)
](https://laurentperrinet.github.io/post/2018-04-10_trames/featured.png)
La vibration des apparences
La vibration des apparences
N_rho, N_phi = 34, 233
def retino_grid(cr, N_rho, N_phi, N_H, N_V, offset, size_mag,
ecc_max, alpha, c1, c2, power, operator,
channel='both'):
cr.scale(N_H, N_V)
cr.set_operator(operator)
# https://laurentperrinet.github.io/sciblog/posts/2020-04-16-creating-an-hexagonal-grid.html
phi_v, rho_v = np.meshgrid(np.linspace(0, 2*np.pi, N_phi, endpoint=False),
np.linspace(0, ecc_max, N_rho+1, endpoint=True)[1:], sparse=False, indexing='xy')
phi_v[::2, :] += np.pi/N_phi
offsets = [-offset, offset]
colors = [c1, c2]
for offset_, color in zip(offsets, colors):
# convert to cartesian coordinates
X = rho_v * np.sin(phi_v) + offset_
Y = rho_v * np.cos(phi_v)
X = (X+1)/2
Y = (Y+1)/2
R = size_mag * rho_v**power / N_rho
# draw
for x, y, r in zip(X.ravel(), Y.ravel(), R.ravel()):
circle(cr, x, y, r)
cr.set_source_rgba(*hue_to_rgba(color, alpha))
cr.fill()
return cr
c_blue = 240
dc = 60
opts = dict(N_rho=N_rho, N_phi=N_phi, N_H=N_H, N_V=N_V,
offset=0.07, size_mag=0.3, ecc_max=0.8, alpha=0.80, c1=c_blue-dc, c2=c_blue+dc, power=.5, operator=cairo.OPERATOR_MULTIPLY)
@disp
def draw(cr, N_H=N_H, N_V=N_V): cr = retino_grid(cr, **opts)
](https://laurentperrinet.github.io/talk/2025-04-18-vibration-apparences/2024-09-04_canaux_both.png)
La vibration des apparences
La vibration des apparences
Laurent Perrinet
Journées d’Ouverture Scientifique (JOS)
[2025-04-18]
