This manuscript (permalink) was automatically generated from laurentperrinet/Perrinet20PredictiveProcessing_manubot@e2e176c on April 13, 2021.

Authors

• Laurent U Perrinet · https://laurentperrinet.github.io/
  0000-0002-9536-010X · laurentperrinet · laurentperrinet
  Institut de Neurosciences de la Timone, CNRS / Aix-Marseille Université · Funded by ANR project “Horizontal-V1” N°ANR-17-CE37-0006.

Abstract

Within the central nervous system, visual areas are essential in transforming the raw luminous signal into a representation which efficiently conveys information about the environment. This process is constrained by the necessity of being robust and rapid. Indeed, there exists both a wide variety of potential changes in the geometrical characteristics of the visual scene and also a necessity to be able to respond as quickly as possible to the incoming sensory stream, for instance to drive a movement of the eyes to the location of a potential danger. Decades of study in neurophysiology and psychophysics at the different levels of vision have shown that this system takes advantage of a priori knowledge about the structure of visual information, such as the regularity in the shape and motion of visual objects. As such, the predictive processing framework offers a unified theory to explain a variety of visual mechanisms. However, we still lack a global normative approach unifying those mechanisms and we will review here some recent and promising approaches. First, we will describe Active Inference, a form of predictive processing equipped with the ability to actively sample the visual space. Then, we will extend this paradigm to the case where information is distributed on a topography, such as is the case for retinotopically organized visual areas. In particular, we will compare such models in light of recent neurophysiological data showing the role of traveling waves in shaping visual processing. Finally, we will propose some lines of research to understand how these functional models may be implemented at the neural level. In particular, we will review potential models of cortical processing in terms of prototypical micro-circuits. These allow to separate the different flows of information, from feed-forward prediction error to feed-back anticipation error. Still, the design of such a generic predictive processing circuit is still not fully understood and we will enumerate some possible implementations using biomimetic neural networks.

Motivation: Role of dynamics in the neural computations underlying visual processing

Vision, the capacity of making sense of the luminous environment, is traditionally thought as a sequence of processing steps from the retinal input to some higher-level representation. It is often thought that this sequence of independent processing steps, or “pipeline”, is implemented by a feedforward process in the visual pathways, through the thalamus and then to the visual areas within the cerebral cortex. Such a model of vision is sufficient to explain the simple detection of the printed character you are currently looking at, and thus for the reading of a full sentence. Indeed, such an ability involves rapid and unconscious low-level processes. Importantly, such ability in humans is also largely immune to changes in luminance (like a shadow on this page) or to geometrical deformations, such as when reading this text from a slanted perspective. More generally, vision will correctly complete the image of a word with missing letters or with ambiguous or incorrect detections due to an overlapping clutter. Such a robustness is characteristic of biological systems, hence it’s use as a Turing Test for security algorithms such as CAPTCHAs. In contrast, models of vision as implemented in computers can learn complex categorization tasks on very precise datasets but are easily outperformed by an infant when it comes to a naturalistic, flexible, and generic context. Going even further, human vision is also characterized by higher-level processes and allows for prospective predictions such as those revealed during mental imagery —and is a basic ground stone for one’s creativity, or imagination. Vision is thus a highly complex process, yet, it is still not completely understood. As a matter of fact, the most surprising fact about vision is the ease with which sighted persons may perform these abilities. To rephrase [1], “the Unreasonable Effectiveness of Vision in the Natural World” invites us to focus on this cognitive ability for a better understanding of the brain in general.

Anatomically, vision is the result of the interplay of neural networks which are organized in a hierarchy of visual areas. Each visual area is itself a dynamical process, from its first stage, the retina, to the efferent visual areas which help in forming a parallel and distributed representation of the visual world. Moreover, this organization is largely self-organized and very efficient metabolic-wise. To make sense of such complex network of visual areas, it has been proposed that this system is organized such that it efficiently predicts sensory data [2]. This ecological approach [3] allows to explain many aspects of vision as predictive processing. Such an approach takes different forms such as redundancy reduction [4], maximization of information transfer [5] or minimization of metabolic energy. Formalizing such optimization strategies in probabilistic language, these may be encompassed by the “Bayesian Brain” framework [6]. More generally, it is possible to link these different theories into a single framework, the Free Energy Principle (FEP) [7]. This principle constitutes a crucial paradigm shift to study predictive processes at both philosophical and scientific levels. Key to this principle is the notion that, knowing the processes that generated the visual image and the internal generative model that allows its representation, predictive processes will take advantage of a priori knowledge to form an optimal representation of the visual scene [8]. This knowledge constitutes an explicit (probabilistic) representation of the structure of the world. For instance, an image which is composed of edges will be understood at a higher level using the a priori knowledge of the link between any individual edges to form a representation of the contours of visual objects. In the time domain, the knowledge of geometric transforms such as the motion of visual objects will help predict their future positions and to ultimately track the different bits of motion, but also to represent contours invariantly to this motion.

However, there are limits and constraints to the efficiency of vision. First, luminous information can be noisy and ambiguous, such as in dim light conditions. This constrains the system to be robust to uncertainties. This highlights a key advantage of predictive processing as this involves learning a generative model of sensory data. On the one hand, by explicitly representing the precision of variables (the inverse of the inferred variance of its value), one can optimally integrate distributed information, even in the case that this uncertainty is not uniform and dynamically evolving in the system. On the other hand, a generative model allows to explicitly represent transformations of the data (such as a geometrical transform of the image like a translation or a rotation) and therefore to make predictions about future states. Second, neural networks have limited information transfer capacities and always need some delay to convey and process information. In humans for instance, the delay for the transmission of retinal information to the cortex is approximately 50 milliseconds, while the minimal latency to perform an oculomotor action is approximately an additional 50 milliseconds [9] (see [10] for equivalent values in monkeys). While this naturally constrains the capacity of the visual system, we will herein take advantage of these delays to dissect the different visual processes. In particular, we will focus in this chapter on the role of these fundamental temporal constraints on the dynamics of predictive processes as they unravel with the passage of time.

To illustrate the challenge of representing a dynamic signal, let’s use the example of the recording of a set of neural cells in some visual areas. Let’s assume that these recordings are evoked by an analog visual signal (as a luminous signal projected on a population of retinal sensory cells) and that we may extract the analog timings of spiking events for a population of cells. We may then choose to display this data in a “raster plot”, that is, showing the timing of the spikes for each of the identified cell. Time is thus relative to that of the experimenter and is given thanks to an external clock: It is shown a posteriori, that is, after the recording. In general, this definition of an absolute time was first formalized by Newton and defines most of the laws of physics, using time as an external parameter. But there is yet no evidence that neurons would have access to a central clock which gives a reference to the absolute, physical time. Rather, neural responses are solely controlled by the present distribution of electro-chemical gradients on their membrane, potentially modulated by neighboring cells. Such a notion of time is local to each neuron and its surrounding. As a consequence, the network’s dynamics is largely asynchronous, that is, timing is decentralized. Moreover, this local notion of (processing) time is a priori disjoint from the external time which is used to represent the visual signal. Such an observation is essential in understanding the principles guiding the organization of visual processes: A neural theory of predictive processes can be only defined in this local (interoceptive) time, using only locally available information at the present instant. In particular, we will propose that neural processes in vision aim at “predicting the present” [11] by using an internal generative model of the visual work and using sensory data to validate this internal representation.

This chapter will review such dynamical predictive processing approaches for vision at different scales of analysis, from the whole system to intermediate representations and finally to neurons (following in a decreasing order the levels of analysis from [12]). First, we will apply the FEP to vision as a normative approach. Furthermore, visual representations should handle geometrical transformations (such as the motion of a visual object) but also sensory modifications, such as with eye movements. Extending the previous principle with the capacity of actively sampling sensory input, we will define Active Inference (AI) and illustrate its potential role in understanding vision, and also behaviors such as eye movements (see Section 2). Then, we will extend it to understand how such processes may be implemented in retinotopic maps (see Section 3). In particular, we will show how such a model may explain a visual illusion, the Flash-lag effect. This will then be compared with neurophysiological data. Finally, we will review possible implementations of such models in Spiking Neural Networks (see Section 4). In particular, we will review some models of elementary micro-circuits and detail some potential rules for learning the structure of their connections in an unsupervised manner. We will conclude by synthesizing these results and their limits.

Active Inference and the “optimality” of vision

Optimization principles seem the only choice to understand “The Unreasonable Effectiveness of Vision in the Natural World”. However, trying to understand vision as an emergent process from efficiency principle seems like a teleological principle in which causation would be reversed [13]. Still, the “use of the teleological principle is but one way, not the whole or the only way, by which we may seek to learn how things came to be, and to take their places in the harmonious complexity of the world.” [14]. Putting this another way, it is not of scientific importance to know if the brain is using explicitly such a principle (for instance that some of its parts may use Bayes’s rule), but rather that such a set of rules offers a simpler explanation for the neural recordings by shedding light on processes occurring in this complex system [15]. We will follow basic principles of self-organized behavior: namely, the imperative to predict at best sensory data, that is, in technical terms, to minimize the entropy of hidden states of the world and their sensory consequences.

Perceptions as hypotheses, Actions as experiments

For instance, it is not yet known why the fast mechanism that directs our gaze toward any position in (visual) space, the saccadic system, is at the same time fast and flexible. For instance, this system may quickly adapt for contextual cues, for instance when instructing the observer to count faces in a painting. Most theories will explain such mechanisms using sensory or motor control models, yet few theories integrate the system as a whole. In that perspective, the FEP provides with an elegant solution. As a first step, we will consider a simplistic agent that senses a subset of the visual scene as its projection on the retinotopic space. The agent has the ability to direct his gaze using saccades. Equipping the agent with the ability to actively sample the visual world enables us to explore the idea that actions (saccadic eye movements) are optimal experiments, by which the agent seeks to confirm predictive models of the hidden world. This is reminiscent of Helmholtz’s definition of perception [16] as hypothesis testing [17]. This provides a plausible model of visual search that can be motivated from the basic principles of self-organized behavior. In mathematical terms, this imperative to maximize the outcome of predicted actions is equivalent to minimizing the entropy of hidden states of the world and their sensory consequences. This imperative is met if agents sample hidden states of the world efficiently. In practice, once the generative model is defined; this efficient sampling of salient information can be derived using approximate Bayesian inference and variational free energy minimization [7]. One key ingredient to this process is the (internal) representation of counterfactual predictions, that is, of the probable consequences of possible hypothesis as they would be realized into actions. This augments models of an agent using the FEP such as to define Active Inference (AI).

Using the SPM simulation environment [18], Friston and colleagues [19] provide simulations of the behavior of such an agent which senses images of faces, and knowing an internal model of their structure. In modeling the agent, they clearly delineate the hidden external state (the visual image, the actual position of the eye or motor command) from the internal state of the agent. Those internal beliefs are linked by a probabilistic dependency graph that is referred to as the generative model. Applying the FEP to this generative model translates (or compiles in computer science terms) to a set of differential equations with respect to the dynamics of internal beliefs and the counterfactual actions. An agent forms expectations over sensory consequences it expects in the future under each possible action. This formulation of active inference forms what is called a Markov decision process [20]. As a system following the FEP, this process is predictive. Yet, it extends the classical predictive processing of Rao and Ballard [8] by including action (and priors related to motor commands) to the overall optimization scheme. The chosen action is the one which is expected to reduce sensory surprise and is ultimately realized by a reflex arc.

Simulations of the resulting AI scheme reproduce sequential eye movements that are reminiscent of empirically observed saccades and provide some counterintuitive insights into the way that sensory evidence is accumulated or assimilated into beliefs about the world. In particular, knowing the localized image sensed on the retina, saccades will explore points of interests (eyes, mouth, nose) until an internal representation of the whole image is made. This AI process allows to bridge the image in intrinsic (retinal) coordinates with extrinsic world coordinates which are prevalent in visual perception but actually hidden to the agent. Interestingly, if one were to only look at the behavior of this agent, this could be encompassed by a set of differential equations, but that would miss the causal relationship with internal variables as defined above. In addition, this model highlights a solution to a common misconception about FEP as surprise minimization. Indeed, if the agent was to close his eyes, the sensory surprise would be minimal as one would then precisely expect a pitch-dark visual scene. However, in the graph of dependencies (i.e., generative model) which defines the agent, such a counterfactual (prospective) hypothesis would be highly penalized as it would also be a priori known that such an action would not yield a minimization of the surprise about the visual scene. Globally, it is therefore more ecological to keep eyes open to explore the different parts of the visual scene.

Is there a neural implementation for Active Inference (AI)?

As we have seen above, once we have resolved the optimization problem given the whole setting (generative model, priors) the agent that we have defined is simply ruled by a set of differential equations governing its dynamics. Technically, these equations are the result of a generic approximation on the form of the internal representation. In particular, the optimization problem is simplified when using the Laplace approximation, that is, when internal beliefs are represented by multidimensional Gaussian probability distribution functions. This holds true in all generality when transforming variables in higher dimensions, such is the case for generalized coordinates [21]. Such coordinates represent at any (present) time the Taylor expansion of the temporal trajectory of any variable, that is the vector containing the position, velocity, acceleration, and further motion orders. Consequently, the solution provided by these equations gives a plausible neural implementation as a set of hierarchically organized linear / non-linear equations [22]. In particular these equations are the Kalman-Bucy filtering solution [23] which provides with a Bayes-optimal estimate of hidden states and actions in generalized coordinates of motion. This generalizes the predictive coding framework offered by [8] for explaining the processing mechanisms in the primary visual cortex. Similar to that model, the dynamical evolution of activity at the different levels of the hierarchy is governed by the balance in the integration of internal (past) beliefs with (present) sensory information [22]. In particular, the relative weights assigned to the modulation of information passing are proportional to the (inferred) precision of each individual variable in the dependency graph. This allows us to predict the influence of the prior knowledge of precision at any given level on the final outcome.

Practically, the predictive power of AI in modeling such an agent is revealed by studying deviations from the typical behavior within a population of agents. For instance, there are acute differences in the smooth pursuit eye movements (SPEM) between patients from (control) neurotypic or schizophrenic groups. First, SPEM are distinct from the saccades defined above as they are voluntary eye movements which aim at stabilizing the retinal image of a smoothly moving visual object. For a target following the motion of a pendulum for instance, the eye will produce a prototypical response to follow this predictable target. Interestingly, schizophrenic agents tend to produce a different pattern of SPEM in the case that the pendulum is occluded on half cycles (for instance, as it passes behind an opaque cardboard on one side from the midline). In general, SPEM may still follow the target, as it is occluded (behind the cardboard) yet with a lower gain [24]. As the target reappears from behind the occluder, schizophrenic agents engage more quickly to a SPEM response [25]. Extending the agent modeled in [19], an agent which has the capability to smoothly follow such moving object was modeled in [26]. This model allows in particular to understand most prototypical SPEM as a Bayes-optimal solution to minimize surprise in the perception / action loop implemented in the agent’s dependency graph.

Especially, by manipulating the a priori precision of internal beliefs at the different levels of the hierarchical model, one could reproduce different classes of SPEM behaviors which reproduce classical psychophysical stimuli. For instance, [26] found for the half-cycle occluded pendulum that manipulating the post-synaptic gain of predictive neurons reproduced behaviors observed in schizophrenia and control populations. Such a difference in the balance of information flow could have for instance a genetic origin in the expression of this gain and vicariously in the behavior of this population. Importantly, such a method thus allows to perform quantitative predictions: Such applications of computational neuroscience seem particularly relevant for a better understanding of the diversity of behaviors in the human population (see for instance [27,28]).

Introducing delays in AI: dynamics of predictive processing

An interesting perspective to study the role of neural dynamics in cognition is to extend this model to a more realistic description of naturalistic constraints faced by the visual system. Indeed, the central nervous system has to contend with axonal delays, both at the sensory and at the motor levels. As we saw in the introduction, it takes approximately 50 milliseconds for the retinal image to reach the visual areas implicated in motion detection, and a further 50 milliseconds to reach the oculomotor muscles and actually realize action [9]. One challenge for modeling the human visuo-oculomotor system is to understand eye movements as a problem of optimal motor control under axonal delays. Let’s take the example of a tennis player trying to intercept a passing-shot ball at a (conservative) speed of 20 m/s. The position sensed on the retinal space corresponds to the instant when the image was formed on the photoreceptors within the retina, and until it reaches our hypothetical motion perception area. At this instant, the sensed physical position is in fact lagging 1 meter behind, that is, approximately at an eccentricity of 45 degrees. However, the position at the moment of emitting the motor command will be also 45 degrees ahead of its present physical position in visual space. As a consequence, if the player’s gaze is not directed to the image of the ball on the retina but to the ball at its present (physical) position, this may be because he takes into account, in an anticipatory fashion, the distance the ball travels during the sensory delay. Alternatively, optimal control may direct action (future motion of the eye) to the expected position when motor commands reach the periphery (muscles). Such an example illustrates that even with such relatively short delay, the visual system is faced with significant perturbations leading to ambiguous choices. This ambiguity is obviously an interesting challenge for modeling predictive processing in the visual system.

Extending the modeling framework of [26] for SPEM, it was observed in [29] that representing hidden states in generalized coordinates provides a simple way of compensating for both delays. A novelty of this approach is to include the delays in the dynamics by taking advantage of generalized coordinates. Technically, this defines a linear operator on those variables to travel back and forth in time with arbitrary intervals of time, allowing in particular to represent the state variables in the past (sensory delay) or in the future (motor delay). Note that (1) this representation is active at the present time, (2) it allows for the concomitant representation of precision of state variables, and (3) this allows for the evaluation of counterfactual hypothesis of sensory states (based on past sensory states) and of an action which has to be inferred now, knowing it will be effective after the motor delay. Applying such an operator to the FEP generates a slightly different and more complicated mathematical formulation. However, it is important to note that to compensate for delays, there is no change in the structure of the network but just in how the synaptic weights are tuned (similar to what we had done in the first section of this chapter): “Neurobiologically, the application of delay operators just means changing synaptic connection strengths to take different mixtures of generalized sensations and their prediction errors.” [29]. In particular, when the agent has some belief about these delays, it can Bayes-optimally integrate internal beliefs. Such a behavior is still regulated by the same type of internal equation.

We illustrated the efficacy of this scheme using neuronal simulations of pursuit initiation responses, with and without compensation. Figure [1 (A)] reports the conditional estimates of hidden states and causes during the simulation of pursuit initiation, using a simple sweep of a visual target, while compensating for sensory motor delays. Here, we see horizontal excursions of oculomotor angle (blue line) and the angular position of the target (dashed black line). One can see clearly the initial displacement of the target that is suppressed after a few hundred milliseconds. This figure also illustrates the effects of sensorimotor delays on pursuit initiation (red lines) in relation to compensated (optimal) active inference. Under pure sensory delays (dotted line), one can see clearly the delay in sensory predictions, in relation to the true inputs. Of note here is the failure of optimal control with oscillatory fluctuations in oculomotor trajectories, which become unstable under combined sensorimotor delays.

Interestingly, this model extends to more complex visual trajectories. In particular, it has been shown that gaze will be directed at the present physical position of the target (thus in an anticipatory fashion) if that target follows a smooth trajectory (such as a pendulum). More striking, this is also true if the trajectory is predictable, for instance for a pendulum behind a static occluder [24,26]. Figure [1 (B)] reports the simulation of smooth pursuit when target’s motion is hemi-sinusoidal, as would happen for a pendulum that would be stopped at each half cycle, left of the vertical. Note that contrary to the agent modeled in [26], this agent has the biological constraint that sensory and motor processing is delayed. The generative model has been equipped with a second hierarchical level that contains hidden states that account for the latent periodic behavior of target motion. One can clearly see the initial displacement of the target that is suppressed after a few hundred milliseconds (pink shaded area). The improvement in pursuit accuracy is apparent at the onset of the second cycle of motion, similar to psychophysical experiments [24]. Indeed, the model has an internal representation of latent causes of target motion that can be called upon even when these causes are not expressed explicitly (occluded) in the target trajectory. A particular advantage of this model is that it provides a solution for the integration of past and future information while still being governed by online differential equations. This therefore implements some form of Bayes-optimal temporal memory.

Summary

To sum up, we have shown here that a full visual perception / action cycle could be understood as a predictive process under the Active Inference (AI) framework. In particular, we have shown that such models could reproduce the dynamics observed in eye movements, in particular when introducing realistic constraints such as sensory-motor delays. Further models should allow for the introduction of even more complex structural constraints such as the physical laws governing the motion of visual objects such as an a priori bias [30], gravity, or external cues [31]. This may help synthesize most laws governing the organization of perception, as formalized in the Gestalt theory.

Predictive processing on visual maps

While we have shown the role of predictive processing at a macroscopic scale by designing each neural assembly as a node in a dependency graph, is there any evidence for such processes in visual space?

The flash-lag effect as evidence for predictive processing in topographic maps

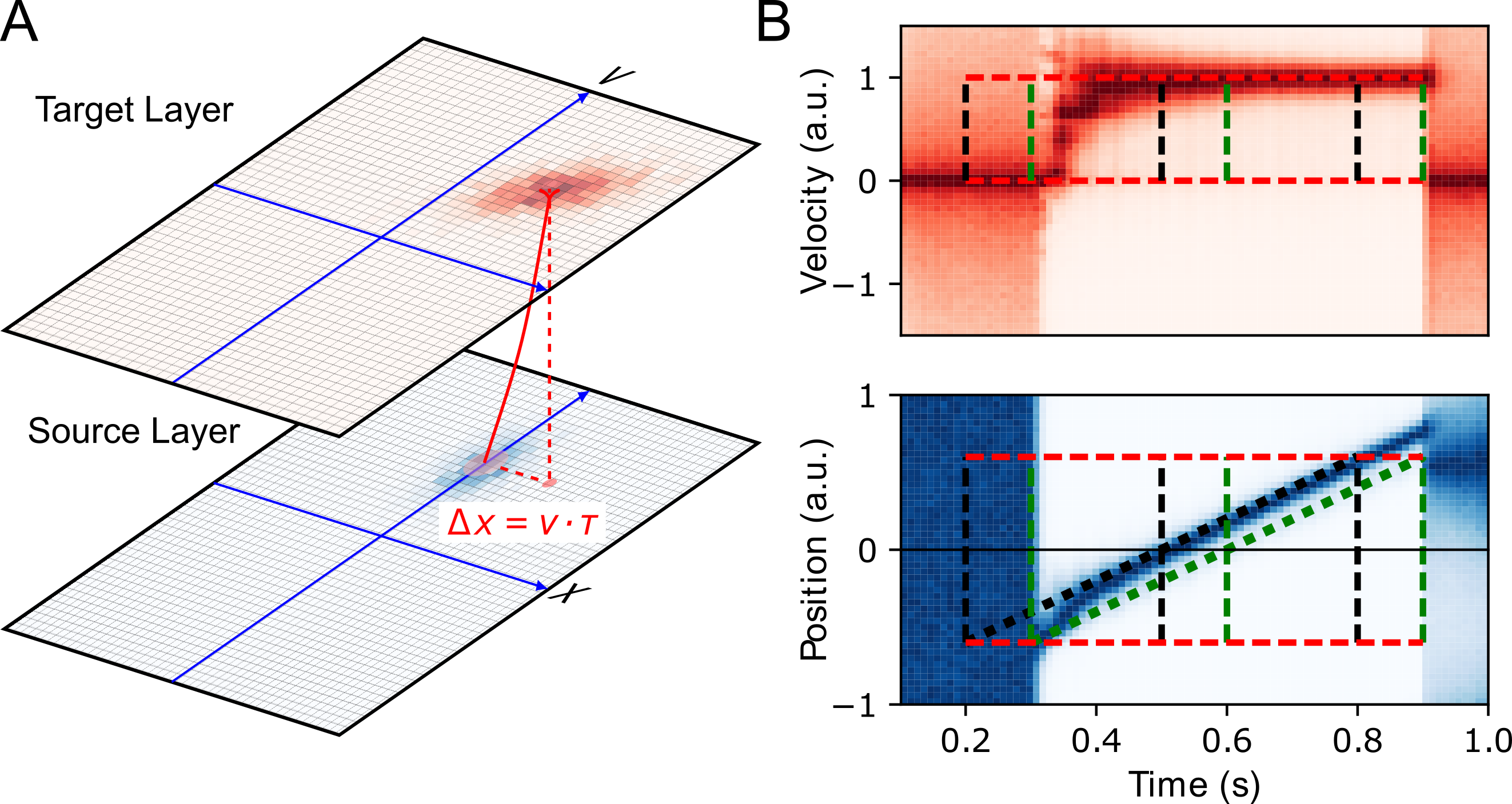
The flash-lag effect (FLE) is a visual illusion which is popular for its generality and simplicity. In its original form [33], the observer is asked to keep fixating at a central cross on the screen while a dot traverses it with a constant, horizontal motion. As it reaches the center of the screen, another dot is briefly flashed just below the moving dot. While they are vertically perfectly aligned, the flashed dot is perceived as lagging the moving dot. This visual illusion saw a resurgence of scientific interest with the motion extrapolation model [34,35]. However, other models such as differential latency or postdiction were also proposed, such that it is yet not clear what is the neural substrate of the FLE. Here, extending the model compensating for delays [29], we define a model of predictive processing generalized on the visual topography using an internal representation of visual motion [36] to define an anisotropic diffusion of information [2 (A)].

The model that we used for the FLE can be used with any image. In particular, a single flashed dot evokes an expanding then contracting isotropic activity while a moving dot may produce a soliton-like wave which may traverse an occlusion [37]. More generally, this model may be described as a simplification of the Navier Stokes equation of fluid dynamics using the advection term. As such, solutions to these equations are typically waves which are traveling on the retinotopic map. A particular feature of these maps is that these include an amplification term for rectilinear motions. As a consequence, once an object begins to be tracked, its position is predicted in the future, such that position and velocity are better estimated. On the contrary, a dot which is moving on an unpredictable trajectory is explained away by the system. This explains some of the non-linear, switch-like behaviors explained by this model [36]. It is of particular interest at this point to understand if such a model extends to other stimuli or if we can precise its neural correlate.

Applied to the image of the FLE, activity in the model shows three different phases; see [2 (B)]. First, there is a rapid build-up of the precision of the target after the first appearance of the moving dot (at 300 milliseconds). Consistently with the Fröhlich effect [38], the beginning of the trajectory is seen ahead of its physical position. During the second phase, the moving dot is efficiently tracked as both its velocity and its position are correctly inferred. This is ahead of the delayed trajectory of the dot (green dotted line). Motion extrapolation correctly predicts the position at the present time and the position follows the actual physical position of the dot (black dotted line). Finally, the third phase corresponds to motion termination. The moving dot disappears and the corresponding activity vanishes in the source layer at t=900 milliseconds. However, between t=800 milliseconds and t=900 milliseconds, the dot position was extrapolated and predicted ahead of the terminal position. At t=900 milliseconds, while motion information is absent, the position information is still transiently consistent and extrapolated using a broad, centered prior distribution of speeds: Although it is less precise, this position of the dot at flash termination is therefore, with hindsight, not perceived as leading the flash.

Neural correlate of apparent motion

Let’s apply a similar approach to another visual illusion: When two stationary dots are flashed at close successive positions and times, observers may experience a percept of motion. This transforms the presentation of a discrete pattern into a continuous one. This visual illusion is called apparent motion and can persist over a relatively long range (superior to the characteristic size of the RF of a neuron in the primary visual cortex, V1). Similarly to the study above for the FLE, it is believed that this long-range Apparent Motion (lrAM) can be explained by predictive processes. Due to the dynamical characteristics of lrAM, a neural implementation of this illusion may consist in the propagation of visual information through intra-cortical interactions. In particular, these lateral interactions may evoke waves of activity in V1 which may modulate the integration of the sensory information coming from thalamocortical connections. An interesting prospect is thus to record neural activity during the presentation of the lrAM stimulus. This allows to quantitatively assess why the superposition of two dots as in lrAM is “more” than the sum of the two dots in isolation.

In a recent study [39], we used VSDI to record the activity of the primary visual cortex (V1) of awake macaque monkeys. Is there any difference between the response to the single dot and that to the two dots? Indeed, VSDI recordings allow to record the activity of populations of V1 neurons which are approximately at the scale of a cortical column. In addition, the recorded response is rapid enough to capture the dynamics of the lrAM stimulus. Recordings show that as the evoked activity of the second stimulus reaches V1, a cortical suppressive wave propagates toward the retinotopic wave evoked by the first dot. This was put in evidence by statistically comparing the response of the brain to the response of the two dots in isolation. In particular, we found that thanks to this suppressive wave, the activity for the brain stimulus was more precise, suggesting that such suppressive wave could serve as a predictive processing step to be read-out in upstream cortical areas.

In particular, we found that the activity that we recorded fitted well with a mean-field model using a dynamical gain control. Qualitatively, this model reproduced the propagation of activity on the cortex. Importantly, this model allowed to show that the observed activity was best fitted when the speed of lateral connections within the mean-field was about 1 m/s, a propagation speed which is of the order of that measured for intra-cortical connections in the primary visual cortex (for a review, see [40]). A more functional (probabilistic) model also showed that the cortical suppressive wave allowed to disambiguate the stimulus by explaining away (i. e. suppressing) ambiguous alternatives. As a consequence, (1) lateral interactions are key to generate traveling waves on the surface of the cortex and (2) these waves help disambiguate the input stimulus. This corresponds to the implementation of a predictive process using an a priori knowledge of smoothly-moving visual objects.

Summary

As a summary, we have seen that it is possible to extend predictive processing to topographic maps. In particular, the resulting computations are particularly adapted to vision. We have shown (see [2]) a model which represents (at any given present time) different variables (here “Source” and “Target”). In a more realistic model, neural activity is more likely to form intermediate representations between past, present and also future representations [41] and at different levels of adaptation as illustrated for the lrAM stimulus [39]. As a consequence, such processes are observed phenomenologically as the propagation of neural information tangentially to the cortical surface, modulating dynamically the feed-forward and feed-back streams. In particular it is an open question whether such neural computations could be implemented by traveling waves on the cortical surface [40].

Open problems in the science of visual predictive processing

In Section 2, we have studied the dynamics of predictive processing at the macroscopic scale, that is, by considering (cortical) areas as nodes of a dependency graph. In Section 3, we have extended such models within such nodes as fields organized on the topography of each visual area. At an even finer scale than this intermediate mesoscopic scale is the microscopic scale of actual neural cells. To better understand the mechanisms of predictive processing, we will now finesse the granularity of the modeling to this scale. In particular, in addition to the asynchronous nature of the neural representation that we explored above, communication between neurons has the property of being event-based. Indeed, the vast majority of neural cells across the living kingdom communicate using prototypical, short pulses called action potentials or spikes. In this section, we will propose three open problems which are raised when modeling such Spiking Neural Networks (SNNs) in the context of predictive processing.

The challenges of representing visual information in Spiking Neural Networks (SNNs)

Following the first generations of Artificial Neural Networks (ANNs), present machine learning algorithms such as Deep Learning (DL) algorithms constitute a breakthrough which formed a second generation of ANNs. SNNs constitute a potential, third generation [42]. Indeed, event-based representation have many advantages which are a deadlock in DL. For instance, instead of repeating all compu­tations for each layer, channel and pixel of a hierarchical ANN, and for which energy-greedy GPUs are necessary, event-based computations need only to be performed for active units at the time of a spike. In particular, a fast developing area of research consists in developing dedicated hardware, such as neuromorphic chips, which would allow to scale the effective volume of computations beyond the last generations of classical semi-conductors (CPUs, GPUs) which attain the limits of Moore’s Law.

Crucial in this new type of representation is on one hand the discrete nature of the addressing of neurons and on the other hand the analog nature of the timing of spikes. Notable results using such architectures have been made in real-time classification and sensor fusion [43] and in pattern recognition [44]. Indeed, an important property of SNNs is the ability to dynamically encode a latent, internal variable (the membrane potential in neuro-physiology) and to emit a spike when (and only when) an internally defined threshold is reached. This defines each spiking neuron as an integrator (similarly to classical neurons), but also potentially as a synchrony detector [45]. This ability to modulate the processing based on the relative timing of presynaptic spikes constitutes a novel paradigm for neural computations [46]. In particular, this shows that the balance in the flux of incoming excitatory and inhibitory spikes is crucial to maximize the efficiency of such SNNs [47].

The role of cortical waves in shaping the dynamic processing of visual information

Another crucial point in deciphering the predictive processing mechanisms is given by the functional anatomy. Indeed, in the primary visual cortex (V1) as in other cortical areas, the neural network is highly recurrent with a median number of 10000 connections per neuron. Surprisingly, 95 percent of these connections occur within a 2mm radius (macaque monkey) [48]. This suggests that a majority of neural resources is devoted to intra-areal communications. One putative functional role of this dense network is to generate traveling waves which modulate the strength and dynamics of the incoming feed-forward neural activity [40]. We have seen its potential role in disambiguating motion [39] and it has also been shown to facilitate the progressive build-up of visual information [49]. Previously, we have successfully modeled such a predictive process [32,36,37], and implemented it in a SNN [50].

One “holy grail” in that direction is to find canonical micro-circuits for predictive coding [51]. This follows from the observation that across species and areas, the cortex seems to follow some prototypical, layered structure. In the particular case of V1, while the thalamic input reaches mostly the (intermediate) granular layer, a feed-forward stream is mostly propagated to efferent layers through the supra-granular layers while feed-back is in majority mediated by infra-granular layers. This anatomical segregation could correspond to different types of signals in predictive coding, respectively expected states and prediction error [51]. Such basic micro-circuits have been applied to explain the response of V1 neurons to natural scenes [52] by using a push-pull mechanism. Still it is an open problem as to know how such a circuitry may emerge.

Integrative properties of cortical areas: toward sparse, efficient representations

Another interesting perspective is the integrative nature of neural computations. While it was believed that neurons would represent the combination of visual features, this is in general not correct [53]. Instead, it has been found that activity may become sharper as visual features are accumulated. For instance, [54] has shown that neurons in cat’s area 17 respond more selectively when presenting natural images (which consist locally to a sum of edges) compared to a single edge. Recently, [55] has shown that a similar result may occur in rodents as soon as in the retina. Behaviorally, this fits also with the observation in humans that more complex textures are driving more robustly eye movements [55]. Such phenomena are consistent with the predictive processing principle that by accumulating coherent information, the a posteriori probability (and hence the response of the system) gets more precise.

Strikingly, this translates in the neural activity by the fact that for a more coherent set of inputs, the neural activity of the population is more sparse [54,56]. This was already explained by the predictive coding model of [8] and implemented in [52] for instance. Importantly, the principle of sparse coding is itself sufficient to (1) explain in a principled fashion much of gain-control mechanisms [22] and (2) guide the learning of the connectivity within a population of neurons, such as in V1 [57,58,59]. This helps to solve an important problem, that is, that the system is self-organized and that the learning of the connectivity should be unsupervised. As such, the plasticity rules that should be developed in SNNs should use similar governing principles.

However, we still lack realistic models of such visual predictive processing. We have built a simplified model which is able to process static images [60]. It consists of a multi-layered neural network, where each layer includes both a recursive intra-cortical mechanism to generate sparse representations and also the ability for each layer to integrate (feedback) information from a higher-level layer. The main novelty of this network is that it allows for the unsupervised learning of the convolutional kernels within each layer. Compared to classical Convolutional Neural Networks such as commonly found in deep learning architectures, we found that the emerging kernels were more meaningful: For instance, when learning on a class of images from human faces, we observed in the second layer different neurons sensitive to face features such as eye, mouth or nose. This is similar to what is found in the fusiform face area, but more simulations are needed to validate the emergence of this representation. Moreover, these simulations are computationally intensive and prohibit their use on conventional computer architectures. A translation of this algorithm into a SNN would therefore be highly beneficial and allow for its application to a dynamical stream of images.

Summary and conclusions

As a summary, we have reviewed in this chapter different models of predictive coding applied to vision. We have seen at a macroscopic scale the role of dynamics using Active Inference (see Section 2). Extending such model to a retinotopic map, we could describe a functional traveling wave to disambiguate visual stimuli (see Section 3). However, we have also shown a limit of such models at the microscopic scale (see Section 4). In particular, it is not yet understood at the single cell level how (1) information is represented in spiking activity, (2) what is the functional role of traveling waves on cortical surfaces (3) if a common efficiency principle (such as sparse coding) could be used to guide the organization of such highly recurrent networks into a single universal circuit.

To further extend our knowledge of predictive processing in vision (see Section 4), it thus seems necessary to be able to implement full-scale SNNs implementing complex visual processes. However, the three different anatomical scales that we have highlighted above (feed-forward, lateral, feedback) seem to be tightly coupled and can be difficult to be modeled separately. More generally, this is also true for the scales that we have defined, from the macroscopic, to the mesoscopic and microscopic. As such, it is highly difficult to produce models which are simple enough to be useful for our understanding of the underlying processing [15,61]. For instance, after deducing them from optimization principles, all the models that we have presented here are pre-connected: The hyper-parameters controlling the interconnection of neurons are fixed. Though we have provided with simulations showing the role of these hyper-parameters, it seems necessary for a better understanding to further explore their relative effects. In particular, we envision that such self-organized architectures could define time as an emerging variable synchronizing predictive processes at the multiple levels of visual processing.

Indeed, a normative theory for predictive processing should provide not only a possible solution (one given model with one set of hyper parameters) but with an exploration of all possible solutions. One first methodology is to have a complete understanding of the set of models using mathematical analysis. However, this becomes impossible for such complex systems and using simplifying assumptions often leads to a shallow complexity. Another venue is to develop adaptive strategies to explore the functional space of different models. This can be for instance developed using machine learning techniques such as the stochastic gradient descent commonly used in deep learning. Another promising solution is to explore bio-inspired adaptive strategies. Those exist at different time scales, from rapid adaption mechanisms, to a slower learning of connections, or to the long-term evolution of hyper-parameters. In particular, it is yet not completely understood how SNNs perform a spike-time dependent plasticity. This sets a future challenge in our understanding of the science of predictive processes in vision.

Acknowledgments

This work was supported by ANR project “Horizontal-V1” N°ANR-17-CE37-0006. The author would like to thank Berk Mirza, Hugo Ladret and Manivannan Subramaniyan for careful reading and insightful remarks.

References