Sparse representations
Laurent Perrinet
NeuroSchool PhD Program in Neuroscience
[2024-04-17]

Sparse representations?

Sparse representations in computer vision
]](https://laurentperrinet.github.io/publication/perrinet-04-tauc/featured.png)

Sparse representations in computer vision

Sparse representations in computer vision
Sparse representations in computer vision
]](https://laurentperrinet.github.io/sciblog/files/2021-03-27_generative.png)
Sparse representations in neuromorphic engineering

Sparse representations in neuromorphic engineering

Sparse representations in neuromorphic engineering
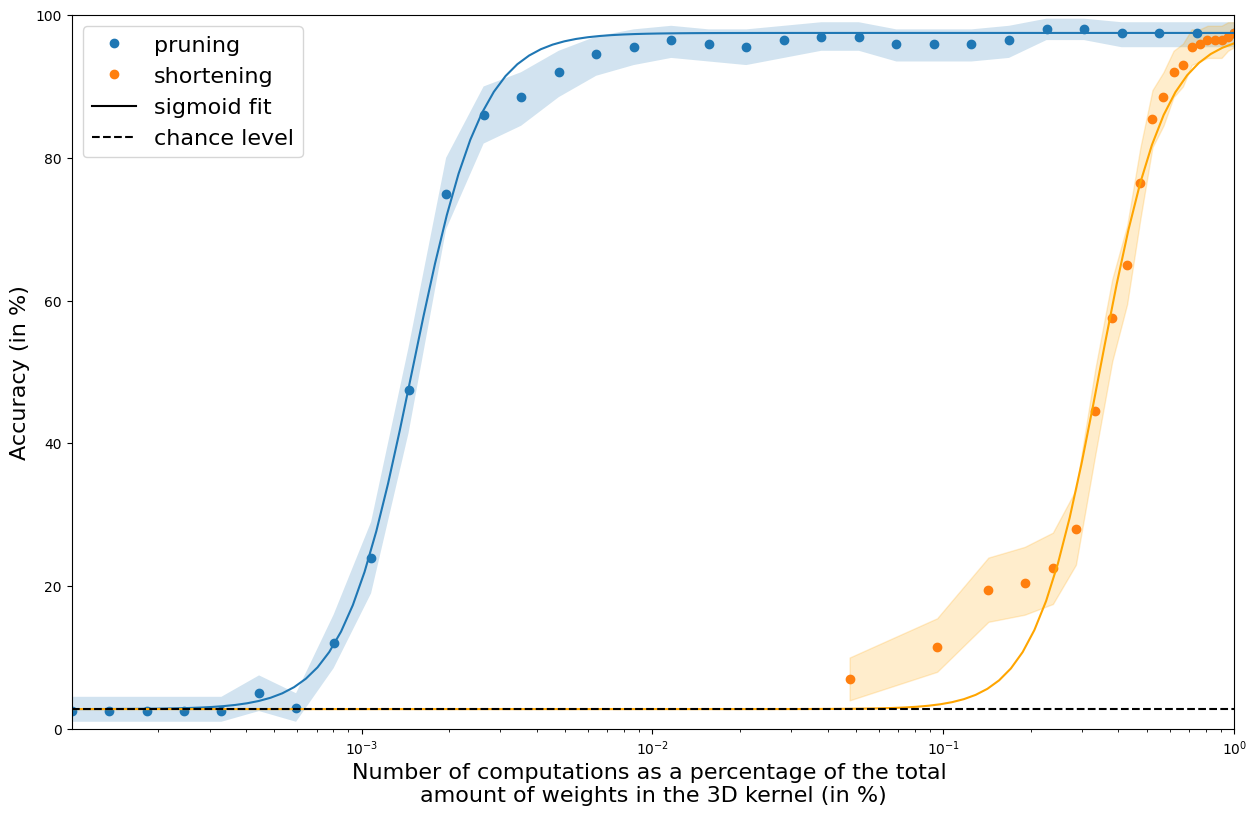
Sparse representations in neuroscience
]](https://laurentperrinet.github.io/2019-04-03_a_course_on_vision_and_modelization/figures/Brunel200Fig2.png)
Sparse representations in neuroscience
]](https://github.com/SpikeAI/2022_polychronies-review/raw/main/figures/replicating_MainenSejnowski1995.png)
Sparse representations in neuroscience
]](https://laurentperrinet.github.io/2019-04-03_a_course_on_vision_and_modelization/figures/fncir-10-00037-g001a.jpg)
Sparse representations in neuroscience
]](https://laurentperrinet.github.io/2019-04-03_a_course_on_vision_and_modelization/figures/fncir-10-00037-g001b.jpg)
Sparse representations in neuroscience
]](https://laurentperrinet.github.io/2019-04-03_a_course_on_vision_and_modelization/figures/fncir-10-00037-g001.jpg)
Sparse representations?

Sparse representations in a nutshell

Sparse representations in a nutshell
]](https://laurentperrinet.github.io/publication/perrinet-04-tauc/featured.png)
Sparse representations in a nutshell
]](https://laurentperrinet.github.io/2019-04-03_a_course_on_vision_and_modelization/figures/Olshausen_2.png)
Sparse representations in a nutshell
Generative model of image synthesis:
$I[x, y] = $ $\sum_{i=1}^{K} a[i] \cdot \phi[i, x, y]$ $ + \varepsilon[x, y]$
Where $\phi$ is a dictionary of $K$ atoms, $a$ is a sparse vector of coefficients, and $\varepsilon$ is a noise term.Sparse representations in a nutshell
]](https://laurentperrinet.github.io/2019-04-03_a_course_on_vision_and_modelization/figures/Olshausen_1.png)
Sparse representations in a nutshell
Given an observation $I$,
$$ \begin{aligned} \mathcal{L}(a) & = - \log Pr( a | I ) \\ \end{aligned} $$
Sparse representations in a nutshell
Given an observation $I$,
$$ \begin{aligned} \mathcal{L}(a) & = - \log Pr( a | I ) \\ & = - \log Pr( I | a ) - \log Pr(a) \\ \end{aligned} $$
Sparse representations in a nutshell
Given an observation $I$,
$$ \begin{aligned} \mathcal{L}(a) & = - \log Pr( a | I ) \\ & = - \log Pr( I | a ) - \log Pr(a) \\ & = \frac{1}{2\sigma_n^2} \sum_{x, y} ( I[x, y] - \sum_{i=1}^{K} a[i] \cdot \phi[i, x, y])^2 - \sum_{i=1}^{K} \log Pr( a[i] ) \end{aligned} $$
Sparse representations in a nutshell
The problem is formalized as an optimization problem $a^\ast = \arg \min_a \mathcal{L}(a)$ with:
$$ \mathcal{L} = \frac{1}{2} \sum_{x, y} ( I[x, y] - \sum_{i=1}^{K} a[i] \cdot \phi[i, x, y])^2 + \lambda \cdot \sum_i ( a[i] \neq 0) $$
Sparse representations in a nutshell
The problem is formalized as an optimization problem $a^\ast = \arg \min_a \mathcal{L}(a)$ with:
$$ \mathcal{L}(a) = \frac{1}{2} \sum_{x, y} ( I[x, y] - \sum_{i=1}^{K} a[i] \cdot \phi[i, x, y])^2 + \lambda \cdot \sum_{i=1}^{K} | a[i] | $$
Sparse representations in a nutshell
]](https://laurentperrinet.github.io/publication/rentzeperis-23/featured.png)
Sparse representations in a nutshell
]](https://laurentperrinet.github.io/2019-04-03_a_course_on_vision_and_modelization/figures/Olshausen_5.png)
Matching pursuit algorithm
Init : Residual $R = I$, sparse vector $a$ such that $\forall i$, $a[i] = 0$
while $\frac{1}{2} \sum_{x, y} R[x, y]^2 > \vartheta $, do :
Matching pursuit algorithm
Init : $R = I$, $\forall i$, $a[i] = 0$
while $\frac{1}{2} \sum_{x, y} R[x, y]^2 > \vartheta $, do :
- compute $c[i] = \sum_{x, y} (R[x, y] - a[i] \cdot \phi[i, x, y])^2$
- Match: $i^\ast = \arg \min_i c[i]$
Matching pursuit algorithm
Init : $R = I$, $\forall i$, $a[i] = 0$
while $\frac{1}{2} \sum_{x, y} R[x, y]^2 > \vartheta $, do :
- Match : $i^\ast = \arg \max_i \sum_{x, y} R[x, y] \cdot \phi[i, x, y]$
Matching pursuit algorithm
Init : $R = I$, $\forall i$, $a[i] = 0$
while $\frac{1}{2} \sum_{x, y} R[x, y]^2 > \vartheta $, do :
- Match : $i^\ast = \arg \max_i \sum_{x, y} ( I[x, y] \cdot \phi[i, x, y])$
- Assign : $a[i^\ast] = \frac{\sum_{x, y} R[x, y] \cdot \phi[i^\ast, x, y]}{\sum_{x, y} \phi[i^\ast, x, y] \cdot \phi[i^\ast, x, y]}$
Matching pursuit algorithm
Init : $R = I$, $\forall i$, $a[i] = 0$, and normalize $\sum_{x, y} \phi[i, x, y]^2 = 1$
while $\frac{1}{2} \sum_{x, y} R[x, y]^2 > \vartheta $, do :
- Match : $i^\ast = \arg \max_i \sum_{x, y} R[x, y] \cdot \phi[i, x, y]$
- Assign : $a[i^\ast] = \sum_{x, y} R[x, y] \cdot \phi[i^\ast, x, y]$
Matching pursuit algorithm
Init : $R = I$, $\forall i$, $a[i] = 0$, $\sum_{x, y} \phi[i, x, y]^2 = 1$
while $\frac{1}{2} \sum_{x, y} R[x, y]^2 > \vartheta $, do :
- Match : $i^\ast = \arg \max_i \sum_{x, y} R[x, y] \cdot \phi[i, x, y]$
- Assign : $a[i^\ast] = \sum_{x, y} R[x, y] \cdot \phi[i^\ast, x, y]$
- Pursuit : $R[x, y] \leftarrow R[x, y] - a[i^\ast] \cdot \phi[i^\ast, x, y]$
Matching pursuit algorithm
Init : $R = I$, $\forall i$, $a[i] = 0$, $\sum_{x, y} \phi[i, x, y]^2 = 1$
compute $c[i] = \sum_{x, y} R[x, y] \cdot \phi[i, x, y]$
compute $X[i, j] = \sum_{x, y} \phi[i, x, y] \cdot \phi[j, x, y]$
while $\frac{1}{2} \sum_{x, y} R[x, y]^2 > \vartheta $, do :
- Match : $i^\ast = \arg \max_i c[i]$
- Assign : $a[i^\ast] = c[i^\ast]$
- Pursuit : $c[i] \leftarrow c[i] - a[i^\ast] \cdot X[i, i^\ast] $
Matching pursuit algorithm
Matching pursuit algorithm
Hebbian learning (once the sparse code is known):
$$ \phi_{i}[x, y] \leftarrow \phi_{i}[x, y] + \eta \cdot a[i] \cdot (I[x, y] - \sum_{i=1}^{K} a[i] \cdot \phi_{i}[x, y] ) $$
Matching pursuit algorithm
Sparse representations in a nutshell
]](https://laurentperrinet.github.io/publication/perrinet-04-tauc/featured.png)
Convolutional Sparse Coding
]](https://laurentperrinet.github.io/publication/boutin-franciosini-chavane-ruffier-perrinet-20/BoutinFranciosiniChavaneRuffierPerrinet20face.png)
Convolutional Neural Nets (CNN)
Convolutional Neural Nets (CNN)
]](https://www.mdpi.com/vision/vision-07-00029/article_deploy/html/images/vision-07-00029-g003.png)
Convolution: Mathematics
- One-dimensional discrete convolution (eg in time) with a kernel $g$ of radius $K$: $$ (f \ast g)[n]=\sum_{m=-K}^{K} f[n-m] \cdot g[m] $$
Convolution: Mathematics
- Convolution of an image (two-dimensional) with a kernel $g$ of radius $K\times K$:
$$ (f \ast g)[x, y] = \sum_{i=-K}^{K} \sum_{j=-K}^{K} f[x-i, y-j] \cdot g[i, j] $$
Convolution: Mathematics
- Cross-correlation of an image (two-dimensional) with a kernel $g$ of radius $K\times K$:
$$ (f \ast \tilde{g})[x, y] = \sum_{i=-K}^{K} \sum_{j=-K}^{K} f[x+i, y+j] \cdot g[i, j] $$
Convolution: Mathematics
]](https://stanford.edu/~shervine/teaching/cs-230/illustrations/convolution-layer-a.png)
Convolution: Mathematics
- Correlation of an image defined on several channels (note the order of the indices):
$$ (f \ast \tilde{g})[x, y] = \sum_{c=1}^{C} \sum_{c,i,j} f[c, x+i, y+j] \cdot g[c, i, j] $$
Convolution: Mathematics
- Correlation of a multi-channel image for multiple output channels (note the order of the indices):
$$ (f \ast \tilde{g})[k, x, y] = \sum_{c,i,j} f[c, x+i, y+j] \cdot g[k, c, i, j] $$
CNN: the HMAX model
![[[Serre and Poggio, 2006]](https://biology.stackexchange.com/questions/10955/ventral-stream-pathway-and-architecture-proposed-by-poggios-group)](https://i.stack.imgur.com/ZlFnp.png)
CNN: challenges
Convolutional Sparse Coding
Convolutional Sparse Coding
Convolutional Sparse Coding
]](https://laurentperrinet.github.io/publication/perrinet-15-bicv/featured.png)
Code @ SparseEdges
Convolutional Sparse Coding
]](https://laurentperrinet.github.io/publication/ladret-23-iclr/fig_dicos.png)
Convolutional Sparse Coding
Convolutional Sparse Coding
]](https://laurentperrinet.github.io/publication/boutin-franciosini-chavane-ruffier-perrinet-20/BoutinFranciosiniChavaneRuffierPerrinet20face.png)
CNN: Predictive processing
]](https://laurentperrinet.github.io/2019-04-03_a_course_on_vision_and_modelization/figures/SDPC_3.png)
CNN: Predictive processing
]](https://laurentperrinet.github.io/2019-04-03_a_course_on_vision_and_modelization/figures/boutin-franciosini-ruffier-perrinet-19_figure4a.png)
CNN: Predictive processing
]](https://laurentperrinet.github.io/2019-04-03_a_course_on_vision_and_modelization/figures/boutin-franciosini-ruffier-perrinet-19_figure4b.png)
CNN: Predictive processing
]](https://laurentperrinet.github.io/publication/boutin-franciosini-chavane-ruffier-perrinet-20/BoutinFranciosiniChavaneRuffierPerrinet20face.png)
CNN: Predictive processing
CNN: Topography
![[Bosking *et al*, 1997]](https://github.com/laurentperrinet/2019-04-03_a_course_on_vision_and_modelization/raw/master/figures/Bosking97Fig4.jpg)
CNN: Topography
]](https://laurentperrinet.github.io/publication/franciosini-21/featured.jpg)
Sparse representations
Laurent Perrinet
NeuroSchool PhD Program in Neuroscience
[2024-04-17]
