Artificial neural networks and machine learning applied to the understanding of biological vision
Laurent Perrinet
[2023-04-03] Master M4NC de l’institut NeuroMod, cours Prospective Innovation and Research.
Principles of Vision
]](https://outde.xyz/img/Rawski/Marr/3Lvls.jpg)
What is the function of vision?
](https://www.cabinetmagazine.org/issues/30/cabinet_030_archibald_sasha_001.jpg)
What is the function of vision?
](https://www.cabinetmagazine.org/issues/30/cabinet_030_archibald_sasha_002.jpg)
What is the function of vision?
](https://www.cabinetmagazine.org/issues/30/cabinet_030_archibald_sasha_003.jpg)
What is the function of vision?
](https://www.cabinetmagazine.org/issues/30/cabinet_030_archibald_sasha_006.jpg)
Visual illusions
Visual illusions
](https://laurentperrinet.github.io/2022-01-12_NeuroCercle/figures/Hering_illusion_without.svg)
Visual illusions
](https://laurentperrinet.github.io/2022-01-12_NeuroCercle/figures/Hering_illusion.svg)
Visual illusions
](https://laurentperrinet.github.io/2022-01-12_NeuroCercle/figures/42_rotsnakes_main.jpg)
Visual illusions : Pareidolia
)](https://laurentperrinet.github.io/2022-01-12_NeuroCercle/figures/Face-on-mars.jpg)
Visual illusions : Pareidolia
)](https://laurentperrinet.github.io/2022-01-12_NeuroCercle/figures/Viking_moc_face_20m_low.png)
Visual illusions : Pareidolia
)](https://laurentperrinet.github.io/2022-01-12_NeuroCercle/figures/Viking_moc_face_20m_high.png)
Principles of vision?
Computational neuroscience of vision
Computational neuroscience of vision
]](https://github.com/laurentperrinet/2019-04-03_a_course_on_vision_and_modelization/raw/master/figures/Churchland92.png)
Anatomy of the Human Visual system
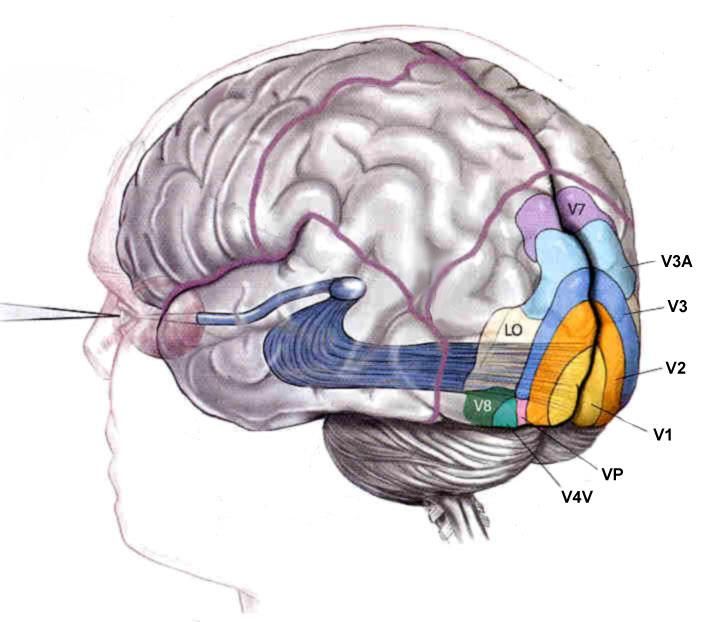
Human Visual system : the HMAX model
]](https://i.stack.imgur.com/ZlFnp.png)
Primary visual cortex: Hubel & Wiesel
![[Hubel & Wiesel, 1962]](https://github.com/laurentperrinet/2019-04-03_a_course_on_vision_and_modelization/raw/master/figures/scientists.jpg)
Primary visual cortex: Hubel & Wiesel
[Hubel & Wiesel, 1962]
Convolutional Neural Networks : Hierarchy
]](https://laurentperrinet.github.io/2019-04-03_a_course_on_vision_and_modelization/figures/boutin-franciosini-ruffier-perrinet-19_figure1_a.svg)
Convolutional Neural Networks : Mathematics
- One-dimensional discrete convolution (eg in time) with a kernel $g$ of radius $K$: $$ (f \ast g)[n]=\sum_{m=-K}^{K} f[n-m] \cdot g[m] $$
Convolutional Neural Networks : Mathematics
- Convolution of an image (two-dimensional) with a kernel $g$ of radius $K\times K$:
$$ (f \ast g)[x, y] = \sum_{i=-K}^{K} \sum_{j=-K}^{K} f[x-i, y-j] \cdot g[i, j] $$
Convolutional Neural Networks : Mathematics
- Cross-correlation of an image (two-dimensional) with a kernel $g$ of radius $K\times K$:
$$ (f \ast \tilde{g})[x, y] = \sum_{i=-K}^{K} \sum_{j=-K}^{K} f[x+i, y+j] \cdot g[i, j] $$
Convolutional Neural Networks : Mathematics
]](https://stanford.edu/~shervine/teaching/cs-230/illustrations/convolution-layer-a.png)
Convolutional Neural Networks : Mathematics
- Correlation of an image defined on several channels (note the order of the indices):
$$ (f \ast \tilde{g})[x, y] = \sum_{c=1}^{C} \sum_{i,j} f[c, x+i, y+j] \cdot g[c, i, j] $$
Convolutional Neural Networks : Mathematics
- Correlation of a multi-channel image for multiple output channels (note the order of the indices):
$$ (f \ast \tilde{g})[k, x, y] = \sum_{c=1}^{C} \sum_{i,j} f[c, x+i, y+j] \cdot g[k, c, i, j] $$
Convolutional Neural Networks : the HMAX model
Convolutional Neural Networks (CNNs)
]](https://www.mdpi.com/vision/vision-07-00029/article_deploy/html/images/vision-07-00029-g003.png)
Convolutional Neural Networks : hierarchy
Convolutional Neural Networks : Predictive coding
]](https://laurentperrinet.github.io/2019-04-03_a_course_on_vision_and_modelization/figures/boutin-franciosini-ruffier-perrinet-19_figure1.svg)
Convolutional Neural Networks : Predictive coding
]](https://laurentperrinet.github.io/publication/boutin-franciosini-chavane-ruffier-perrinet-20/BoutinFranciosiniChavaneRuffierPerrinet20face.png)
Convolutional Neural Networks : Topography
![[Bosking *et al*, 1997]](https://github.com/laurentperrinet/2019-04-03_a_course_on_vision_and_modelization/raw/master/figures/Bosking97Fig4.jpg)
Convolutional Neural Networks : Topography
]](https://laurentperrinet.github.io/publication/franciosini-21/featured.jpg)
Computational neuroscience of vision
Dynamics of vision
Dynamics of vision
).](https://github.com/SpikeAI/2022_polychronies-review/raw/main/figures/visual-latency_bg.jpg)
Dynamics of vision
).](https://github.com/SpikeAI/2022_polychronies-review/raw/main/figures/visual-latency.jpg)
Dynamics of vision
)](https://laurentperrinet.github.io/2022-01-12_NeuroCercle/figures/tsonga.jpg)
Dynamics of vision
)](https://laurentperrinet.github.io/2022-01-12_NeuroCercle/figures/figure-tsonga.jpg)
Dynamics of vision
Dynamics of vision
).](https://github.com/laurentperrinet/Khoei_2017_PLoSCB/raw/master/figures/FLE_DiagonalMarkov.jpg)
Dynamics of vision
Flash-lag effect: MBP (Khoei et al, 2017)
Dynamics of vision
Spiking Neural Networks
Spiking Neural Networks: Leaky Integrate-and-Fire Neuron
.](https://github.com/SpikeAI/2022_polychronies-review/raw/main/figures/LIF.gif)
Spiking Neural Networks in neurobiology
]](http://i.stack.imgur.com/ixnrz.png)
Spiking Neural Networks in neurobiology
]](https://github.com/SpikeAI/2022_polychronies-review/raw/main/figures/replicating_MainenSejnowski1995.png)
Spiking Neural Networks in neurobiology
]](https://github.com/SpikeAI/2022_polychronies-review/raw/main/figures/Diesmann_et_al_1999.png)
Spiking Neural Networks in neurobiology
]](https://github.com/SpikeAI/2022_polychronies-review/raw/main/figures/haimerl2019.jpg)
Spiking Neural Networks: Spiking motifs
.](https://github.com/SpikeAI/2022_polychronies-review/raw/main/figures/izhikevich.png)
Spiking Neural Networks: Spiking motifs
Spiking Neural Networks: Spiking motifs
.](https://github.com/SpikeAI/2022_polychronies-review/raw/main/figures/HSD.gif)
Spiking Neural Networks in neuromorphic engineering
Spiking Neural Networks in neuromorphic engineering
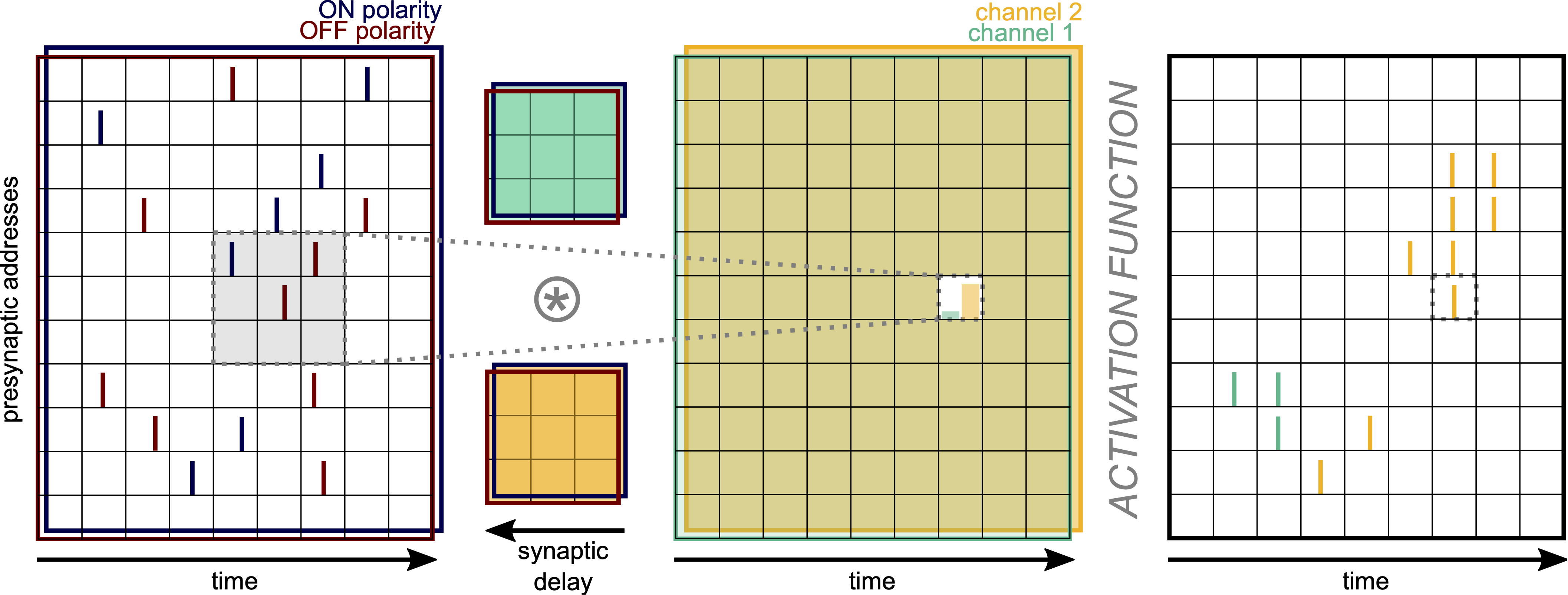
Spiking Neural Networks in neuromorphic engineering
Spiking Neural Networks in neuromorphic engineering
Spiking Neural Networks in neuromorphic engineering
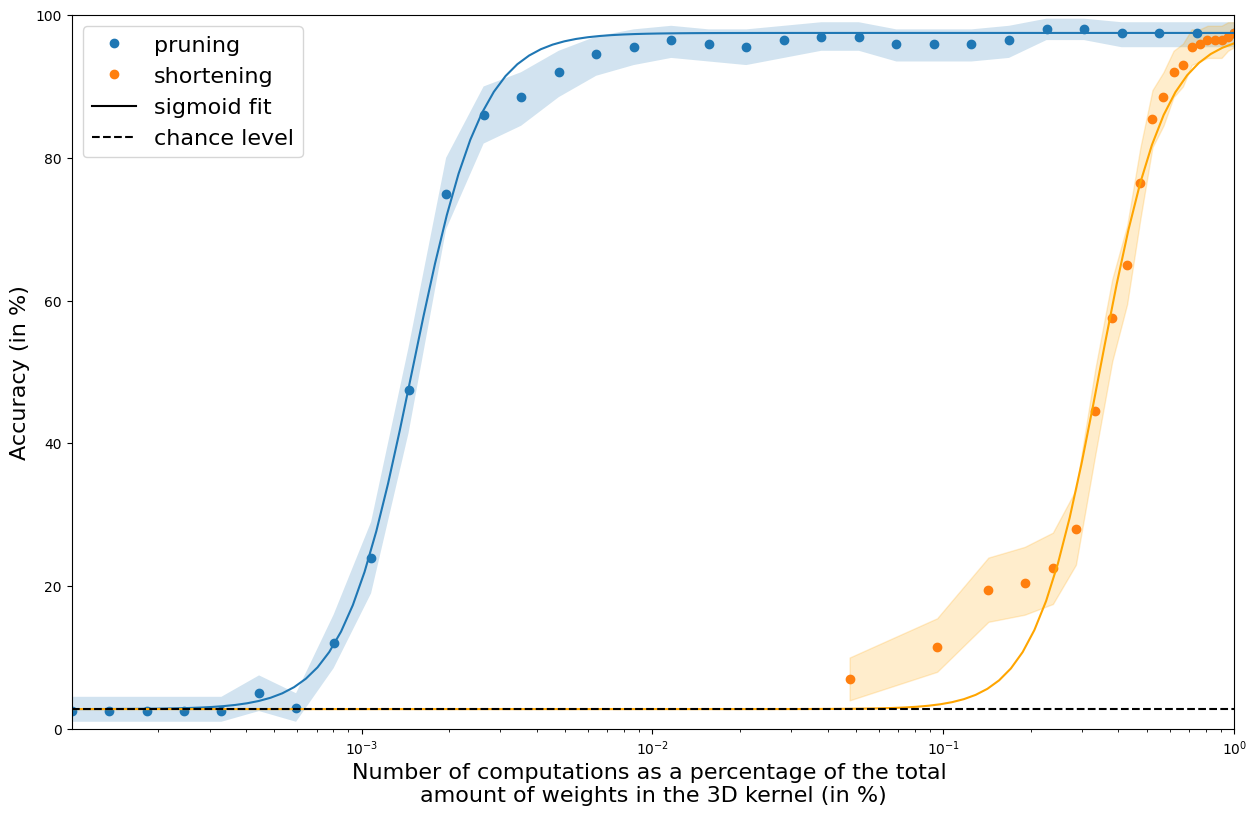
Artificial neural networks and machine learning applied to the understanding of biological vision
Artificial neural networks and machine learning applied to the understanding of biological vision
Laurent Perrinet
[2023-04-03] Master M4NC de l’institut NeuroMod, cours Prospective Innovation and Research.