Réseaux de neurones artificiels et apprentissage machine appliqués à la compréhension de la vision

Laurent Perrinet

[2022-03-23] Master 1 Neurosciences et Sciences Cognitives

Principes de la Vision

À quoi sert la vision?

À quoi sert la vision?

À quoi sert la vision?

À quoi sert la vision?

Les illusions visuelles

Les illusions visuelles

Les illusions visuelles

Ilusions of brightness or lightness Akiyoshi KITAOKA

Les illusions visuelles

Les illusions visuelles : Paréidolie

Les illusions visuelles : Paréidolie

Les illusions visuelles : Paréidolie

Les neurosciences computationnelles

De V1 aux réseaux convolutionnels

Le système visuel

Le cortex visuel primaire

Hubel & Wiesel

[Hubel & Wiesel, 1962]

Réseaux convolutionnels : hiérarchie

Réseaux convolutionnels : Math

• Convolution discrète uni-dimensionnelle (eg dans le temps) avec un noyau f de rayon $K$: $$ (f \ast g)[n]=\sum_{m=-K}^{K} f[m] g[n-m] $$

Réseaux convolutionnels : Math

• Convolution discrète d’une image (bi-dimensionnelle):

$$ (f \ast g)[x, y] = \sum_{i=-K}^{K} \sum_{j=-K}^{K} f[i, j] g[i-x, j-y] $$

Réseaux convolutionnels : l’opération de convolution

Réseaux convolutionnels : Math

• Convolution discrète d’une image sur plusieurs canaux de sortie:

$$ (f \ast g)[x, y, k] = \sum_{i=-K}^{K} \sum_{j=-K}^{K} f[k, i, j, k] g[i-x, j-y] $$

Réseaux convolutionnels : Math

• Convolution discrète d’une image multi-canaux (eg. RGB) sur plusieurs canaux de sortie (noter l’ordre des indices):

$$ (f \ast g)[x, y, k] = \ \sum_{i=-K}^{K} \sum_{j=-K}^{K} \sum_{c=1}^{C} f[k, c, i, j] g[i-x, j-y, c] $$

Réseaux convolutionnels : CNN

Mise en pratique: détecter & apprendre

• Tutoriel Apprentissage profond

• Notebook A_Détecter.ipynb

• Notebook B_Apprendre.ipynb

Perspectives

Réseaux convolutionnels : hiérarchie

Réseaux prédictifs

Topographie dans V1

Spiking Neural Networks

Recurrent processing

Dynamique de la vision

Applications robotiques

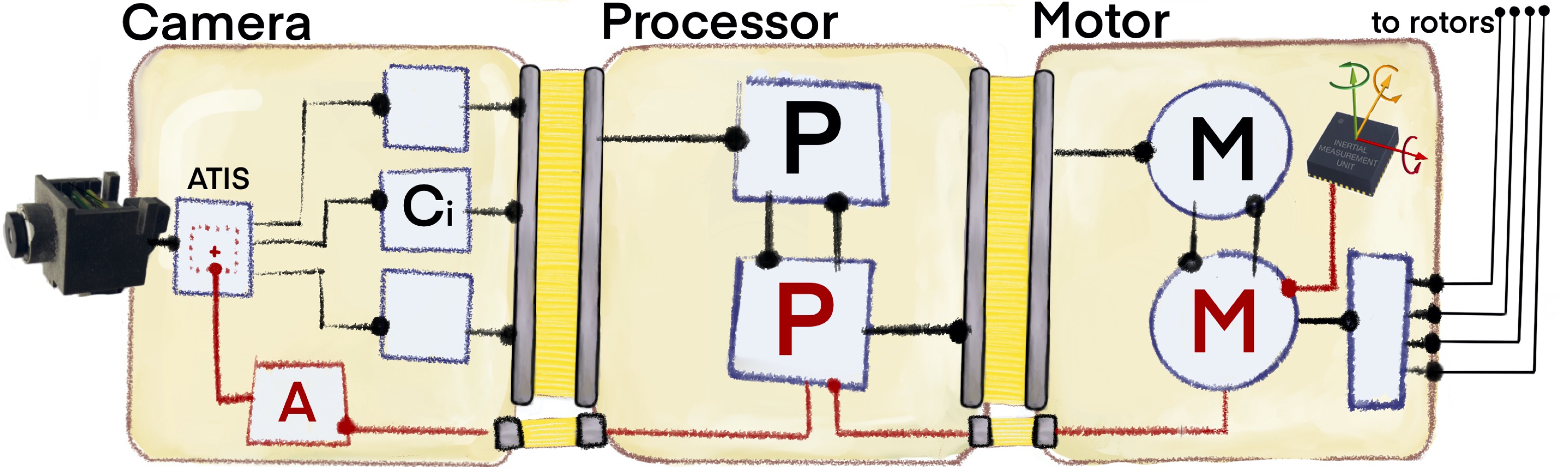
Questions?

Ask info @ laurent.perrinet@univ-amu.fr

More info @ web-site