Modeling of simple cells through a sparse overcomplete gabor wavelet representation based on local inhibition and facilitation
Abstract
We present a biologically plausible model of simple cortical cells as 1) a linear transform representing edges and 2) a non-linear iterative stage of inhibition and facilitation between neighboring coefficients. The linear transform is a complex log-Gabor wavelet transform which is overcomplete (i.e. there are more coefficients than pixels in the image) and has exact reconstruction. The inhibition consists in diminishing down the coefficients which are not at a local-maxima along the direction normal to the edge filter orientation, whereas the facilitation enhances the collinear and co-aligned local-maximum coefficients. At each iteration and after the inhibition and facilitation stages, the reconstructed error is subtracted in the transform domain for keeping an exact reconstruction. Such process concentrates the signal energy on a few coefficients situated along the edges of the objects, yielding a sparse representation. The rationale for such procedure is: (1) th e overcompleteness offers flexibility for activity reassignment; (2) images can be coded by sparse Gabor coefficients located on object edges; (3) image contours produce aligned and collinear local-maxima in the transform domain; (4) the inhibition/facilitation processes are able to extract the contours. The sparse Gabor coefficients are mostly connected each other and located along object contours. Such layout makes chain coding suitable for compression purposes. Specially adapted to Gabor wavelets features, our chain coding represents every chain by its end-points (head and tail) and the elementary movements necessary to walk along the chain from head to tail. Moreover it predicts the module and phase of each Gabor coefficient according to the previous chain coefficient. As a result, redundancy of the transform domain is further reduced. Used for compression, the scheme limits particularly the high-frequency artifacts. The model performs also efficiently in tasks the Human Visual System is supposed to deal with, as for instance edge extraction and image denoising.
- relies on log-Gabor filters:(2007). Self-Invertible 2D Log-Gabor Wavelets. International Journal of Computer Vision.
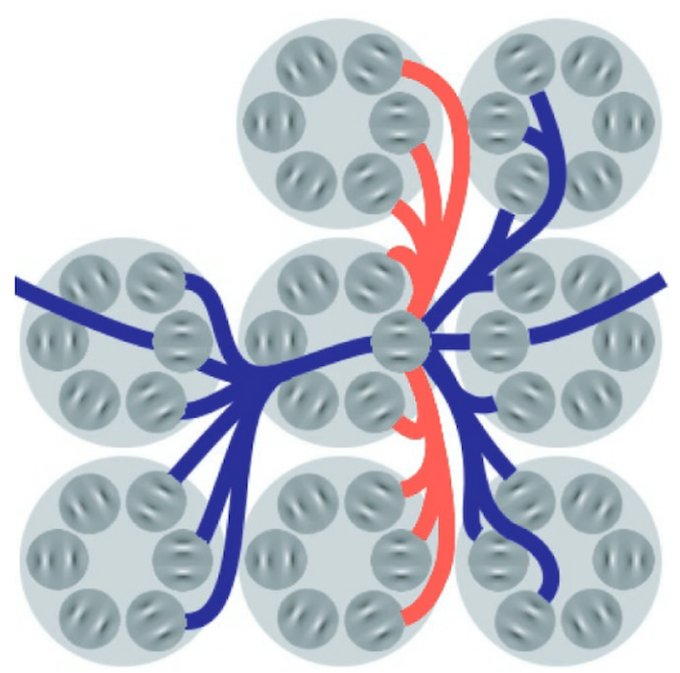
Schematic structure of the primary visual cortex implemented in the present study. Simple cortical cells are modeled through log-Gabor functions. They are organized in pairs in quadrature of phase (dark-gray circles). For each position the set of different orientations compose a pinwheel (large light-gray circles). The retinotopic organization induces that adjacent spatial positions are arranged in adjacent pinwheels. Inhibition interactions occur towards the closest adjacent positions which are in the direc-tions perpendicular to the cell preferred orientation and toward adjacent orientations (light-red connections). Facilitation occurs to-wards co-aligned cells up to a larger distance (dark-blue connections).
Laurent U Perrinet
Researcher in Computational Neuroscience
My research interests include Machine Learning and computational neuroscience applied to Vision.