Abstract
Efficient sparse coding of overcomplete transforms remains still anopen problem. Different methods have been proposed in theliterature, but most of them are limited by a heavy computationalcost and by difficulties to find the optimal solutions. We proposehere an algorithm suitable for Gabor wavelets and based onbiological models. It is composed by local operations betweenneighboring transform coefficients and achieves a sparserepresentation with a relatively low computational cost. Used with achain coder, this sparse Gabor wavelet transform is suitable forimage compression but is also of interest also for otherapplications, in particular for edge and contour extraction andimage denoising.
- relies on log-Gabor filters:(2007). Self-Invertible 2D Log-Gabor Wavelets. International Journal of Computer Vision.
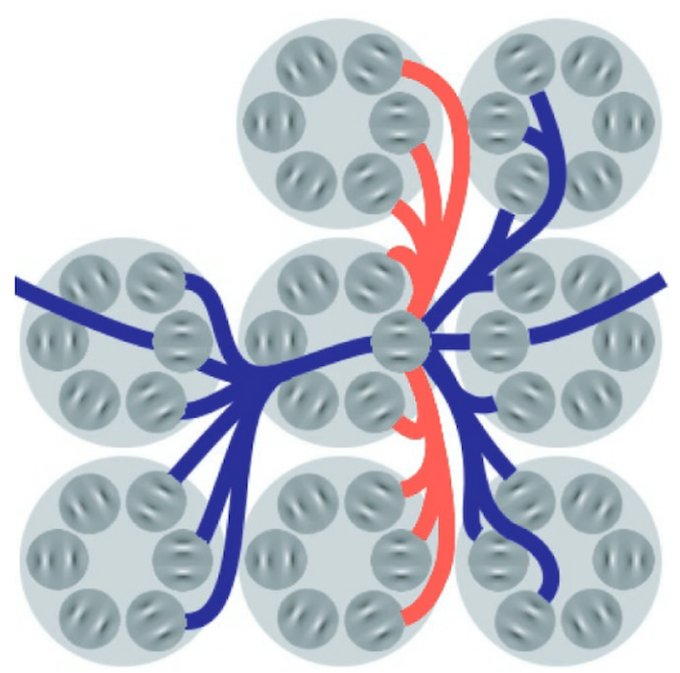
Schematic structure of the primary visual cortex implemented in the present study. Simple cortical cells are modeled through log-Gabor functions. They are organized in pairs in quadrature of phase (dark-gray circles). For each position the set of different orientations compose a pinwheel (large light-gray circles). The retinotopic organization induces that adjacent spatial positions are arranged in adjacent pinwheels. Inhibition interactions occur towards the closest adjacent positions which are in the direc-tions perpendicular to the cell preferred orientation and toward adjacent orientations (light-red connections). Facilitation occurs to-wards co-aligned cells up to a larger distance (dark-blue connections).
Laurent U Perrinet
Researcher in Computational Neuroscience
My research interests include Machine Learning and computational neuroscience applied to Vision.