Dynamics of distributed 1D and 2D motion representations for short-latency ocular following

Abstract

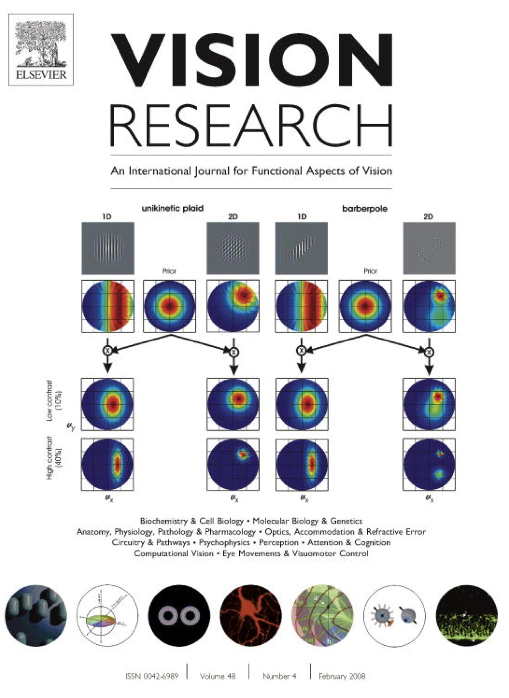
Integrating information is essential to measure the physical 2D motion of a surface from both ambiguous local 1D motion of its elongated edges and non-ambiguous 2D motion of its features such as corners or texture elements. The dynamics of this motion integration shows a complex time course as read from tracking eye movements: first, local 1D motion signals are extracted and pooled to initiate ocular responses, then 2D motion signals are integrated to adjust the tracking direction until it matches the surface motion direction. The nature of these 1D and 2D motion computations are still unclear. One hypothesis is that their different dynamics may be explained from different contrast sensitivities. To test this, we measured contrast-response functions of early, 1D-driven and late, 2D-driven components of ocular following responses to different motion stimuli: gratings, plaids and barberpoles. We found that contrast dynamics of 1D-driven responses are nearly identical across the different stimuli. On the contrary, late 2D-driven components with either plaids or barberpoles have similar latencies but different contrast dynamics. Temporal dynamics of both 1D- and 2D-driven responses demonstrates that the different contrast gains are set very early during the response time course. Running a Bayesian model of motion integration, we show that a large family of contrast-response functions can be predicted from the probability distributions of 1D and 2D motion signals for each stimulus and by the shape of the prior distribution. However, the pure delay (i.e. largely independent upon contrast) observed between 1D- and 2D-motion supports the fact that 1D and 2D probability distributions are computed independently. This two-pathway Bayesian model supports the idea that 1D and 2D mechanisms represent edges and features motion in parallel.

Laurent U Perrinet

Researcher in Computational Neuroscience

My research interests include Machine Learning and computational neuroscience applied to Vision.